Answer

Above we see the cycle plotted both on a $P-V$ and $T-V$ plot. Note that $P_0$ and $V_0$ are the pressure and volume at the end of the first step, not at the beginning!

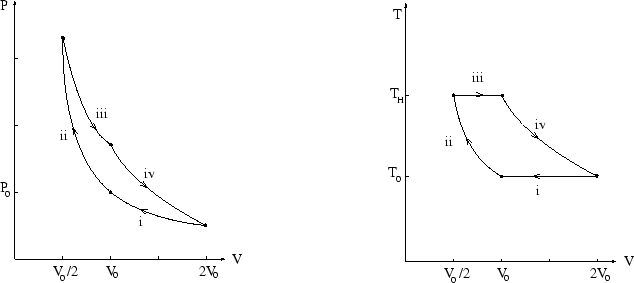
We have already calculated the work done on the gas during an isothermal volume change:

$$W^{\rm isoth}=-nRT_1\ln(V_2/V_1)$$

For the adiabatic stages we use $PV^\gamma={\rm const}$ (see properties of an ideal gas) to get

$$W^{\rm adiab}=-P_1V_1^\gamma\int_{V_1}^{V_2}\frac 1 {V^\gamm......t(\frac {V_1} {V_2}\right)^{\gamma-1}-1\right]= c_V (T_2-T_1)$$

(Note that $nR/(\gamma-1)=c_V$! Can you think of an easier way of obtaining this expression for the work? Hint: no heat is exchanged, so $W=\Delta E$.)

All we need is the temperature of the isothermal expansion, which is also the temperature at the end of the adiabatic compression. Using $TV^{\gamma-1}={\rm const}$ gives $T_2=T_1(V_1/V_2)^{\gamma-1}$ so $T_H =2^{\gamma-1} T_0$ where $T_0=P_0 V_0/nR$.

So

$$\begin{eqnarray*}W^{(i)}&=& -nRT_0\ln (1/2)= nRT_0\ln 2 \\W^{(ii)}&=& c_V(T_H......&=& nR\ln 2(T_0-T_H)= -P_0V_0\ln 2 \Bigl(2^{\gamma-1}-1\Bigr)\end{eqnarray*}$$ The work done by the system is minus this; using $\gamma=5/3$ for a monatomic gas we get 0.407 atmosphere-litres or 41.3 J.

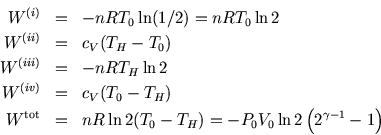
The work done during the adiabatic steps (ii) and (iv) cancels. We could have guessed this, as the work done by the system during the cycle must equal the net heat absorbed. Heat is only absorbed or given out in the isothermal steps, and its magnitude is equal and opposite to the work done on the system in those steps. So we could more simply have written $W^{\rm tot}=-(Q^{(i)}+Q^{(iii)})=W^{(i)}+W^{(iii)}$.