Home: PC 1672 home page |
Up: 4 Rigid-body motion |
Weekly plan |
Help: Guide to using this document |
Next: 4.7 The symmetric top |
Previous: 4.5 Principal axes |
If we use the principal axes as our coordinate axes, the components of the
tensor
![]() form a diagonal matrix
form a diagonal matrix
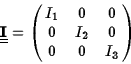
Torque is equal to rate of change of angular momentum in an inertial frame.
In the body-fixed frame (a rotating
frame) this becomes
In terms of coordinate axes that lie along the principal axes
of
![]() ,
the components of the equation of
motion are
,
the components of the equation of
motion are
Textbook references
Home: PC 1672 home page |
Up: 4 Rigid-body motion |
Weekly plan |
Help: Guide to using this document |
Next: 4.7 The symmetric top |
Previous: 4.5 Principal axes |
Mike Birse
17th May 2000