Home: PC 1672 home page |
Up: 2 Noninertial frames . . . |
Weekly plan |
Help: Guide to using this document |
Next: 2.3 Motion on Earth |
Previous: 2.1 Accelerating frames |
PC1672 Advanced dynamics
2.2 Rotating frames
If we choose to work in a frame which is rotating at angular velocity
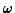 (which for simplicity we will chose to be constant),
then for any vector
(which for simplicity we will chose to be constant),
then for any vector 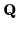 the rate of change which
we observe will differ from the rate of change seen by an inertial observer:
the rate of change which
we observe will differ from the rate of change seen by an inertial observer:
where the subscript 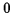 refers to the inertial frame and
refers to the inertial frame and 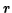 to the rotating
one. The term
to the rotating
one. The term
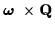 is the rate
at which the vector is carried round by the rotation.
is the rate
at which the vector is carried round by the rotation.
For an object with position 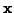 ,
its velocity in the inertial frame
,
its velocity in the inertial frame
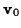 is related to its velocity
is related to its velocity 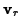 in the rotating frame by
in the rotating frame by
The acceleration in the inertial frame is related to that in our rotating
frame by
In the rotating frame Newton's second law becomes
There are two inertial forces in this case. The first, which depends on
the object's velocity in the rotating frame, is the
Coriolis
force. The second, which depends on the object's position, is the
centrifugal force.
Some instructive
movies
of motion from inertial and rotating points of view have been produced by P. Flament
and coworkers (University of Hawaii).
The centrifugal force
is the more familiar of these two inertial forces.
When the double vector product
is unpacked, it gives of force pointing radially outwards from the axis of
rotation, with magnitude
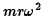 where
where 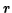 is the distance from the axis.
This contains
is the distance from the axis.
This contains 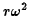 which is just the centripetal
acceleration of an object moving in a circle. (To keep an object moving in a
circle we need to provide a real centripetal force that exactly cancels the
centrifugal force which appears to act on it in the rotating frame.)
which is just the centripetal
acceleration of an object moving in a circle. (To keep an object moving in a
circle we need to provide a real centripetal force that exactly cancels the
centrifugal force which appears to act on it in the rotating frame.)
The Coriolis force
is more subtle in its effects. It is proportional to the object's velocity
and it always acts perpendicularly to the velocity (and to the axis of
rotation). In a frame rotating right-handedly (for example a turntable
spinning anticlockwise when seen from above), the Coriolis force tries to
deflect the motion of an object to the right. In a left-handed (clockwise)
frame, the Coriolis deflection is to the left.
Textbook references
- K&K 8.5, 7.2 example 7.1
- F&C 5.2, 5.3
- B&O 7.1, 7.2
- M 11.1, 11.2
- M&T 10.1, 10.2
Home: PC 1672 home page |
Up: 2 Noninertial frames . . . |
Weekly plan |
Help: Guide to using this document |
Next: 2.3 Motion on Earth |
Previous: 2.1 Accelerating frames |
Mike Birse
23rd March 2001
![]() (which for simplicity we will chose to be constant),
then for any vector
(which for simplicity we will chose to be constant),
then for any vector ![]() the rate of change which
we observe will differ from the rate of change seen by an inertial observer:
the rate of change which
we observe will differ from the rate of change seen by an inertial observer:
![]() ,
its velocity in the inertial frame
,
its velocity in the inertial frame
![]() is related to its velocity
is related to its velocity ![]() in the rotating frame by
in the rotating frame by