

Next: Question *9
Up: Examples 4
Previous: Question 7
A thin circular disc rotates about its centre of mass. It is
subject to a torque which damps rotations about any diameter. The components
of this torque are related to to the components of the angular velocity
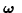 along the principal axes by
along the principal axes by
where 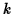 is a constant and the the
is a constant and the the 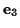 axis has been chosen to be the
one perpendicular to the disc. If the initial angular velocity is not along
a principal axis, determine how
axis has been chosen to be the
one perpendicular to the disc. If the initial angular velocity is not along
a principal axis, determine how 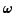 varies with time from the
viewpoint of a body-fixed frame. Try to describe this motion from as seen by a
space-fixed observer, and check this using a Frisbee.
varies with time from the
viewpoint of a body-fixed frame. Try to describe this motion from as seen by a
space-fixed observer, and check this using a Frisbee.
[Hints can be found here, but do not follow this link
until you have attempted the question on your own.]
Mike Birse
2000-03-31
![]() along the principal axes by
along the principal axes by