Hint 4

The fact that the axis of the cylinder is an axis of symmetry means that it must be one of the principal axes. Hence find another two.

The principal moment about the symmetry axis (${\bf e}_3$) is

$$I_3={\pi\rho R^4h\over 2}.$$

The other principal moments are (in cylindrical polars)

$$I_1=I_2 = \rho\int_{-h/2}^{h/2}\int_0^{2\pi}\int_0^R (r^2\sin^2\theta+z^2)\,r\,dr\,d\theta\,dz$$

$$= {\pi\rho R^2h\over 4}\left(R^2+{h^2\over 3}\right)$$

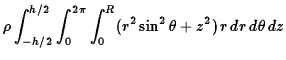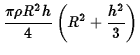In the coordinate system defined by the principal axes, we have $L_i=I_i\omega_i$. For our cylinder this shows that ${\bf L}$ lies in the same plane as $\hbox{{\boldmath$\omega$ }}$ and the symmetry axis, but further from that axis if $h> \sqrt{3} R$.