

Next: Hint 4
Up: Examples 4
Previous: Hint 2
Hint 3
(a) Taking the 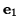 axis along a side of length
axis along a side of length 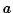 ,
,
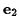 along
along 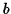 and
and 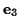 along
along 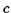 ,
we get
,
we get
and similar expresssions for 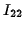 and
and 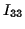 .
.
(b) With a similar choice of axes, in this case we get
By symmetry, the remaining components of the tensor are
Mike Birse
2000-03-31
![]() axis along a side of length
axis along a side of length ![]() ,
,
![]() along
along ![]() and
and ![]() along
along ![]() ,
we get
,
we get