Hint 2

Use the expression for the total inertial force (Coriolis plus centrifugal) on a body in a rotating frame of reference:

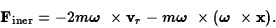$${\bf F}_{\rm iner}=-2m\mbox{\boldmath$\omega$ }\times{\bf v}... ...dmath$\omega$ }\times(\mbox{\boldmath$\omega$ }\times{\bf x}).$$ (1)

You should find that in this example the Coriolis force on the particle points radially outwards when the particle is moving in the same direction as the rotation of the turntable, and radially inwards when the particle is moving in the opposite direction. Adding the centrifugal force, which always points radially outwards, should leave you with a net force of magnitude

$$F_{\rm iner}=\vert m\omega^2r \pm 2m\omega v\vert.$$