

Next: Hint 2
Up: Examples 2
Previous: Question 6
Hint 1
As discussed in the lectures, the apparent gravitational field
at a distance 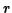 from the axis of rotation is
from the axis of rotation is
At equilibrium, this vector will be normal to the surface of the water. By
considering an infinitessimal tangent vector to the surface,
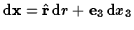 ,
show that
,
show that
and hence integrate to get the parabola
Mike Birse
2000-03-31