

Next: About this document ...
Up: Examples 1
Previous: Hint 7
Hint 8
By symmetry both photons must have the same energy 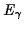 .
Taking the
.
Taking the 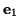 axis to be the direction of the pion's motion, the
4-momenta of the photons are:
axis to be the direction of the pion's motion, the
4-momenta of the photons are:
Conservation of 4-momentum implies that the sum of these is equal to the
4-momentum of the original pion,
Hence energy conservation requires that
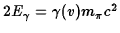 and so
and so
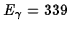 MeV.
MeV.
To find the angle 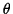 ,
we can square the total 4-momentum to get
,
we can square the total 4-momentum to get
This gives
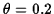 rad. (An alternative method to get
rad. (An alternative method to get 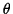 is to use
is to use
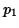 conservation.)
conservation.)
Mike Birse
2001-01-16
![]() .
Taking the
.
Taking the ![]() axis to be the direction of the pion's motion, the
4-momenta of the photons are:
axis to be the direction of the pion's motion, the
4-momenta of the photons are:
![]() ,
we can square the total 4-momentum to get
,
we can square the total 4-momentum to get