

Next: Hint 6
Up: Examples 1
Previous: Hint 4
Hint 5
(a) By conservation of 4-momentum,
where the subscript  refers to the exhaust. Since, for the moment, we are
not interested in the final energy of the rocket, we can rewrite this as an
equation for
refers to the exhaust. Since, for the moment, we are
not interested in the final energy of the rocket, we can rewrite this as an
equation for
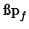 and square both sides to get
and square both sides to get
The initial 4-momentum of the rocket and the 4-momentum of the (massless)
exhaust are
and hence
We can therefore use (1) as an equation for the energy 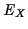 of the exhaust. This
gives
of the exhaust. This
gives
(b) (c) You now have everything you need to write down 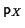 and
and 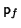 .
.
(d) If the final speed of the rocket is 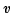 ,
then its energy can be
written in the form
,
then its energy can be
written in the form
Equate this to the final energy you found in part (c) and solve for 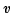 .
.
Mike Birse
2001-01-16
![]() and
and ![]() .
.
![]() ,
then its energy can be
written in the form
,
then its energy can be
written in the form