The 4-momentum
![]() is a 4-vector and so it
transforms just like
is a 4-vector and so it
transforms just like
![]() under a Lorentz transformation.
under a Lorentz transformation.
For a photon
![]() ,
where
,
where ![]() is the frequency of the
photon and
is the frequency of the
photon and ![]() is Planck's constant. If it is moving in the
is Planck's constant. If it is moving in the ![]() direction, then it has
direction, then it has
![]() (and
(and ![]() )
as perceived by
)
as perceived by ![]() .
Boosting this to the frame of
.
Boosting this to the frame of ![]() ,
you should find that the energy
there corresponds to
,
you should find that the energy
there corresponds to
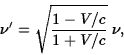
A photon moving in the ![]() direction (in the frame of
direction (in the frame of ![]() )
has
)
has
![]() (and
(and ![]() )
according to
)
according to ![]() .
Boosting to the
frame of
.
Boosting to the
frame of ![]() ,
you should find
,
you should find