PC1672 Advanced dynamics

4.8 Stability of free rotation

Let us now look at free rotations of a general body, with three different principal moments of inertia,

$\begin{displaymath}I_1<I_2<I_3\end{displaymath}$

Note that we have chosen to label these in order of increasing size.

If q body rotates about a principal axis, then it is dynamically balanced: no torque is required to maintain the rotation. Such motion is stable if small perturbations of the axis of rotation just lead to oscillations around the balanced configuration.

To determine whether this is the case, consider a body rotating about an axis very close to one of its principal axes, say the axis ${\bf e}_1$ with the smallest principal moment. The angular velocity can be written

$\begin{displaymath}\hbox{\boldmath {$\omega$}}=\omega_1 {\bf e}_1+\lambda {\bf e}_2 +\mu {\bf e}_3\end{displaymath}$

where $\lambda,\ \mu\ll \omega_1$ . Keeping terms only up to first order in $\lambda$ and $\mu$ , Euler's equations become

$\displaystyle I_1\dot\omega_1$	$\textstyle =$	$\displaystyle 0$
$\displaystyle I_2\dot\lambda+(I_1-I_3)\omega_1\mu$	$\textstyle =$	$\displaystyle 0$
$\displaystyle I_3\dot\mu+(I_2-I_1)\omega_1\lambda$	$\textstyle =$	$\displaystyle 0$

The first equation (which is only approximate) shows that $\omega_1$ is constant. This means that the other two form a pair of coupled linear equations for $\lambda$ and $\mu$ :

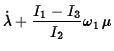$\displaystyle \dot\lambda+{I_1-I_3\over I_2}\omega_1\,\mu$	$\textstyle =$	$\displaystyle 0$
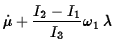$\displaystyle \dot\mu+{I_2-I_1\over I_3}\omega_1\,\lambda$	$\textstyle =$	$\displaystyle 0$

These equations can be decoupled to give an equation for $\lambda$ ,

$\begin{displaymath}\ddot\lambda+{(I_1-I_3)(I_1-I_2)\over I_2 I_3}\omega_1^2\,\lambda=0\end{displaymath}$

The solutions to this are simple harmonic oscillations with frequency

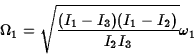
$\begin{displaymath}\Omega_1=\sqrt{(I_1-I_3)(I_1-I_2)\over I_2 I_3}\omega_1\end{displaymath}$

The other component $\mu$ oscillates in a similar way but with a $\pi/2$ phase difference and a different amplitude. The axis of rotation thus executes an elliptical oscillation or precession around the principal axis ${\bf e}_1$ .

The symmetry of Euler's equations under cyclic permutations of the indices means that we can us this to write down the results for small perturbations of rotations about the other two principal axes. In the case of rotations close to ${\bf e}_3$ , the axis with the largest principal moment, the motion is similar to that for ${\bf e}_1$ .

However, rotations close to ${\bf e}_2$ , the axis with the intermediate principal moment, show a quite different behaviour. In this case the ``frequency'' for small perturbations is imaginary. This shows that the solutions are not oscillatory but instead exponential:

$\begin{displaymath}\lambda(t)=Ae^{\alpha_2 t}+Be^{-\alpha_2 t}\end{displaymath}$

where

$\begin{displaymath}\alpha_2=\sqrt{(I_2-I_1)(I_3-I_2)\over I_1 I_3}\omega_2\end{displaymath}$

Hence a small initial perturbation of the axis of rotation away from the ${\bf e}_2$ axis will grow exponentially. Eventually the linear treatment used here breaks down and the full rotational equations need to be solved (using a method known as the Poinsot construction).

This analysis shows that rotations about the principal axes with the largest or smallest moments are stable. In contrast rotations about the principal axis with the intermediate moment are unstable.

Finally, for a body with an axis of symmetry, rotations the symmetry axis are stable, as we saw before. For rotations about the other two principal axes, the frequency of small perturbations is zero. This implies that these rotations are marginally (un)stable: small perturbations do grow with time, but only linearly.

Textbook references

K&K 7.7 example 7.16
F&C (9.4)
B&O 7.7
M 12.11
M&T 11.11

Mike Birse
17th May 2000