Home: PC 1672 home page |
Up: 1 Relativity |
Weekly plan |
Help: Guide to using this document |
Next: 1.5 Relativistic momentum . . . |
Previous: 1.3 Proper time |
The location of an event in space-time can be represented by the 4-vector
![]() where
where
![]() is its position
and
is its position
and
![]() (notation).
This has a meaning which
is the same for all observers, although the four components used to represent
it take different values in different inertial frames. For example, under a
boost to a frame moving with velocity
(notation).
This has a meaning which
is the same for all observers, although the four components used to represent
it take different values in different inertial frames. For example, under a
boost to a frame moving with velocity ![]() in the
in the ![]() -direction introduced before,
the components transform to
-direction introduced before,
the components transform to
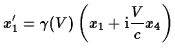 |
|||
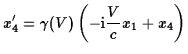 |
Just as the components of all vectors transform in the same way under some rotation of the axes, the components of all four vectors transform in the same way under a particular Lorentz transformation.
All 4-scalars take the same value in all inertial frames. An example is
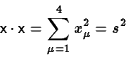
Principle of ovariance: If we express physical laws in terms of 4-scalars and 4-vectors (and in some cases 4-tensors) then these laws will be invariant under Lorentz transformations: they will have the same forms in all inertial frames.
An important example of a 4-vector is the 4-velocity of a particle. This
is defined as the ratio of the change in the particle's space-time position to
the change in its proper time
Another useful 4-vector is
To transform a 4-vector under, for example, the boost in the ![]() -direction,
we simply substitute the components of that 4-vector for the
components of
-direction,
we simply substitute the components of that 4-vector for the
components of ![]() in the expressions above.
This can be applied to the 4-velocity to obtain the
relativistic formula for addition of velocities, and to the wave vector to
get the relativistic Doppler shift.
in the expressions above.
This can be applied to the 4-velocity to obtain the
relativistic formula for addition of velocities, and to the wave vector to
get the relativistic Doppler shift.
Notation: Here sans-serif type will be used to denote 4-vectors, while bold roman type will used for 3-vectors and ordinary type for scalar quantities such as the magnitudes of vectors. See Examples 1 for more details.
Textbook references
Home: PC 1672 home page |
Up: 1 Relativity |
Weekly plan |
Help: Guide to using this document |
Next: 1.5 Relativistic momentum . . . |
Previous: 1.3 Proper time |
Mike Birse
17th May 2000