Home: PC 1672 home page | Up: 1 Relativity | Weekly plan | Help: Guide to using this document |
Next: 1.3 Proper time | Previous: 1.1 Symmetry in physics |

PC1672 Advanced dynamics

1.2 Lorentz invariance

A central feature of Einstein's Special Relativity is that the speed of light is the same in all inertial frames. As a result we have to give up on the idea of a universal time. If an event occurs at position ${\bf x}=(x_1,x_2,x_3)$ and time $t$ as measured by an observer in frame O then for an observer in a frame O' moving with velocity $V$ in the $x_1$-direction it occurs at

    $\displaystyle x'_1 = \gamma(V)(x_1 - Vt)$  
    $\displaystyle x'_2 = x_2$  
    $\displaystyle x'_3 = x_3$  
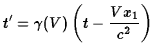    $\displaystyle t' = \gamma(V)\left(t - {Vx_1\over c^2}\right)$  

where

\begin{displaymath}\gamma(V)={1\over\sqrt{1-V^2/c^2}}\end{displaymath}

is the ``time-dilation factor''. (The origins of the coordinate systems in the two frames have chosen to coincide at $t=0$.)

This relation between the space and time coordinates of an event in the two frames is the Lorentz transformation for observers with relative velocity $V$ in the $x_1$-direction. For a Lorentz boost to a frame moving in a general direction, the transformation has a similar form, mixing the coordinate in the boost direction with the time, and leaving the coordinates in perpendicular directions unchanged.

The Lorentz transformation leaves unchanged the quantity

\begin{displaymath}s^2=x_1^2+x_2^2+x_3^2-c^2t^2\end{displaymath}

which defines an invariant distance $s$. This can be interpreted as the distance of an event from the origin in a frame in which the event occurs at $t=0$, assuming that we can find such a frame.

If we introduce the coordinate $x_4={\rm i}ct$ then this invariant can be rewritten as

\begin{displaymath}s^2=x_1^2+x_2^2+x_3^2+x_4^2\end{displaymath}

which looks just like the length squared of a four-component vector. In terms of this rather strange-looking notation, a Lorentz transformation have exactly the form of a rotation of the four-component vector $(x_1,x_2,x_3,x_4={\rm i}ct)$ through an imaginary angle.

We can think of this vector as the position vector of the event in a four-dimensional space-time continuum (often called Minkowski space). In the same way that a real rotation leaves the length of a vector invariant, a Lorentz transformation does not change $s$. To distinguish them from ordinary three-dimensional quantities, we shall refer to these objects as 4-vectors and 4-scalars.

Textbook references

Home: PC 1672 home page | Up: 1 Relativity | Weekly plan | Help: Guide to using this document |
Next: 1.3 Proper time | Previous: 1.1 Symmetry in physics |

Mike Birse
17th May 2000