PC1672 Advanced dynamics

3.11 Space travel

A satellite in low-Earth orbit has energy

$\begin{displaymath}\eta=-{GM_E\over 2R_E}\end{displaymath}$

This corresponds to a speed of

$\begin{displaymath}v=\sqrt{gR_E}=7.9\ \hbox{\rm km s}^{-1}\end{displaymath}$

(where we have use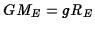

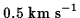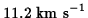). This should be compared with the speed of $0.5\ \hbox{\rm km s}^{-1}$ for an object at rest on the surface of the (rotating) Earth. Also for comparison, the ``escape velocity", the speed needed to escape from the Earth's surface to infinity, is $11.2\ \hbox{\rm km s}^{-1}$ .

To put the satellite into orbit we need to provide it with a kinetic energy of

$\begin{displaymath}{1\over 2}v^2=31\ \hbox{\rm MJ kg}^{-1}\end{displaymath}$

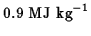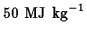This much larger than the potential energy needed to lift it, say, 100 km above the Earth's surface: $0.9\ \hbox{\rm MJ kg}^{-1}$ . For comparison, the energy content of aviation fuel is about $50\ \hbox{\rm MJ kg}^{-1}$ , but remember that we need a supply of oxygen to release this energy.

More details on space travel can found in B&O and on the NASA JPL web site.

Textbook references

K&K 9.6 example 9.6
F&C 6.5
B&O 5.4, 5.5

Mike Birse
17th May 2000