Home: PC 1672 home page | Up: 3 Gravity | Weekly plan | Help: Guide to using this document |
Next: 3.10 Orbital energies | Previous: 3.8 The solar sytem |

PC1672 Advanced dynamics

3.9 Satellites

The same ideas apply to satellites orbiting a planet. For objects in orbit around the Earth (including the Moon), we need the Earth's mass. It is convenient to work with the quantity $GM_E=gR_E^2$ since this can be determined from the gravitational field $g$ here on the Earth's surface. Kepler's third law can then be written in the form

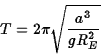
\begin{displaymath}T=2\pi\sqrt{a^3\over gR_E^2}\end{displaymath}

Low-Earth circular orbits have a radius $a\simeq R_E$ (or a couple of hundred km higher to avoid tangling with trees or the atmosphere) and a period of 1.4 hours. Geostationary orbits (used for communications and GPS satellites) are circular with a period of 24 hours and a radius of about $6.6\ R_E$. Hohmann transfer orbits can be used to move satellites from low-Earth to geostationary orbits. These are ellipses whose perigee and apogee distances are equal to the radii of the initial and final circular orbits.

Textbook references

Home: PC 1672 home page | Up: 3 Gravity | Weekly plan | Help: Guide to using this document |
Next: 3.10 Orbital energies | Previous: 3.8 The solar sytem |

Mike Birse
17th May 2000