PC1672 Advanced dynamics

3.7 Orbits

The gravitational potential energy of two objects is

$\begin{displaymath}U(r)=-{GMm\over r}\end{displaymath}$

If the mass of one is much smaller than the other ( $m\ll M$ ) then the reduced mass is approximately equal to the smaller mass ( $\mu\simeq m$ ) and so we can treat the smaller mass as moving in a fixed gravitational field. Its motion is then independent of mass and it is convenient to work in terms of energy and angular momentum per unit mass,

$\begin{displaymath}\eta={E\over m}\qquad\qquad\hbox{\rm and}\qquad\qquad\lambda={L\over m}\end{displaymath}$

In this case the differential equation for the radial motion can be written

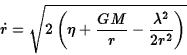
$\begin{displaymath}\dot r=\sqrt{2\left(\eta+{GM\over r}-{\lambda^2\over 2r^2}\right)}\end{displaymath}$

This can be integrated, but only in terms of elliptic integral functions. Alternatively we can combine this equation with

$\begin{displaymath}\dot\theta={\lambda\over r^2}\end{displaymath}$

to get an equation for the shape of the orbit

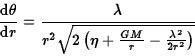
$\begin{displaymath}{{\rm d}\theta\over {\rm d}r}={\lambda\over r^2 \sqrt{2\left(\eta+{GM\over r}-{\lambda^2\over 2r^2}\right)}}\end{displaymath}$

This can be integrated straightforwardly by changing variables to . The result can be written

$\begin{displaymath}r={\alpha\over 1+\epsilon\cos\theta}\end{displaymath}$

where, for simplicity, the constant of integration has been chosen such that the orbit is aligned in the direction $\theta=0$ . The constants in this formula can be expressed in terms of the dynamical quantities $\eta$ and $\lambda$ .

This is the equation of a conic section. (More information and pictures of these curves can be found in Dave's Math Tables and Xah Lee's visual dictionary.) The shape of the curve is determined by the eccentricity $\epsilon$ :

$\epsilon=0$ gives a circle
$\epsilon<1$ gives an ellipse
$\epsilon=1$ gives a parabola
$\epsilon>1$ gives a hyperbola

The orbit of a bound object ( $\eta<0$ ) has $\epsilon<1$ and so it is an ellipse. The size of the ellipse is specified by its semi-major axis ( $a=\alpha/\sqrt{1-\epsilon^2}$ ) and its shape is determined by its eccentricity $\epsilon$ . The centre of force lies at a focus of the ellipse, which is a distance $\epsilon a$ from the centre of the curve. This is Kepler's first law: the orbit of a planet is an ellipse with the Sun at one focus.

An unbound object ( $\eta>0$ ) has $\epsilon>1$ and so follows a hyperbolic orbit. The limiting case is that of an object with only just enough energy to escape ( $\eta=0$ ); its orbit is a parabola, with $\epsilon=1$ .

The minimum distance of an orbiting object from the centre of force is known as the pericentre (perihelion, perigee) distance. For a bound object, this is given by

$\begin{displaymath}r_1=a(1-\epsilon)\end{displaymath}$

while the maximum distance is

$\begin{displaymath}r_2=a(1+\epsilon)\end{displaymath}$

This is known as the apocentre (aphelion, apogee) distance.

The total energy per unit mass of the object is

$\begin{displaymath}\eta=-{GM\over 2a}\end{displaymath}$

Note that this depends only on the size of the orbit

and not on its shape $\epsilon$ (or the angular momentum $\lambda$ ). The energy of an object in an elliptical orbit of semimajor axis

is therefore identical to that for a circular orbit of radius

The period of the orbit can be found from its area $A=\pi ab$ (where $b=a\sqrt{1-\epsilon^2}$ is the semiminor axis of the ellipse) by using Kepler's second law. This gives

$\begin{displaymath}T={2\pi\over\sqrt{GM}}a^{3\over 2}\end{displaymath}$

which is Kepler's third law: the square of the period of a planet's orbit is proportional to the cube of its semimajor axis. Note that this result too is independent of the shape of the orbit and so is identical to the period for a circular orbit of radius

David McNamara and Gianfranco Vidali (Syracuse University) have written a JAVA applet to illustrate orbits in a gravitational field.

Textbook references

K&K 9.6, 9.7
F&C 6.5, 6.6
B&O 5.2, 5.3
M 8.7
M&T 8.7

Mike Birse
27th March 2001