Home: PC 1672 home page |
Up: 3 Gravity |
Weekly plan |
Help: Guide to using this document |
Next: 3.7 Orbits |
Previous: 3.5 Reduced mass |
A conservative central force is obtained from a potential ![]() which
depends only on the radial distance
which
depends only on the radial distance ![]() from the centre
from the centre
A central force is parallel to the position vector ![]() and so the torque
and so the torque
![]() on the object is zero. Since
on the object is zero. Since
![]() ,
the (vector) angular momentum of
the object is constant. Since the angular momentum
,
the (vector) angular momentum of
the object is constant. Since the angular momentum
![]() is perpendicular to
is perpendicular to ![]() and
and
![]() and its direction
is constant, the motion takes place in a plane perpendicular
to
and its direction
is constant, the motion takes place in a plane perpendicular
to ![]() .
.
It is convenient to use plane polar coordinates ![]() and
and ![]() to describe
the motion. In terms of these, the magnitude of
to describe
the motion. In terms of these, the magnitude of ![]() is
is
By considering the area of the triangle swept out by ![]() in a small time,
we find that
in a small time,
we find that ![]() sweeps out area at a rate
sweeps out area at a rate
Since the force is conservative, the total energy
Solving for ![]() in terms of
in terms of ![]() and the constants
and the constants ![]() and
and ![]() ,
we get
,
we get
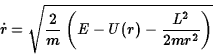
The problem now looks like one-dimensional motion in an effective
potential
Kepler's laws: These three laws describing the motion of the planets were first deduced empirically by Kepler from Tycho Brahe's detailed observations of the motion of Mars. They were then explained by Newton as consequences of his law of gravitation. (For more, see the NASA Kepler site and the St. Andrews history of mathematics archive.)
Textbook references
Home: PC 1672 home page |
Up: 3 Gravity |
Weekly plan |
Help: Guide to using this document |
Next: 3.7 Orbits |
Previous: 3.5 Reduced mass |
Mike Birse
17th May 2000