Home: PC 1672 home page |
Up: 3 Gravity |
Weekly plan |
Help: Guide to using this document |
Next: 4 Rigid-body motion |
Previous: 3.12 Tides |
Matter in the universe as we see it today has a low density and so the gravitational fields acting over large distances are weak. Although a full treatment of the ``geography'' of the universe requires general relativity, we can understand many of its important features using simple Newtonian gravity.
We assume that the universe is uniform on large distance scales, with a density
![]() .
In addition we assume that this matter is now in the form of
``dust'' (consisting of particles as large as stars or even galaxies!) which
means that it does not exert any pressure. In the absence of pressure, the only
force acting on matter is gravity.
.
In addition we assume that this matter is now in the form of
``dust'' (consisting of particles as large as stars or even galaxies!) which
means that it does not exert any pressure. In the absence of pressure, the only
force acting on matter is gravity.
A typical galaxy at some distance ![]() from us feels a gravitational attraction
towards us exerted by all the matter inside a sphere of radius
from us feels a gravitational attraction
towards us exerted by all the matter inside a sphere of radius ![]() centred on
us:
centred on
us:
The total energy of our test galaxy is a constant of its motion. In an
isotropic universe the velocity of the galaxy must point radially with respect
to us. The energy (per unit mass) of the galaxy is
An important special case is that of a universe which is just unbound,
![]() .
In general relativity this corresponds to a universe where space is
flat. In this case the speed of our test galaxy is
.
In general relativity this corresponds to a universe where space is
flat. In this case the speed of our test galaxy is
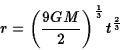
For
![]() things are a bit more complicated but the basic features are
analogous to those of orbits in a gravitational field. If
things are a bit more complicated but the basic features are
analogous to those of orbits in a gravitational field. If ![]() the universe
is bound; any galaxy reaches a maximum distance from us and the universe
eventually collapses in a ``big crunch''. If
the universe
is bound; any galaxy reaches a maximum distance from us and the universe
eventually collapses in a ``big crunch''. If ![]() then the speed at which a
galaxy is moving away from us tends to a constant at large times.
then the speed at which a
galaxy is moving away from us tends to a constant at large times.
Up to a couple of years ago the standard picture of the universe was that the
density of matter was equal to the critical value that makes ![]() exactly
zero. This would also give a flat space (in which a straight line is the
shortest distance between two points). The idea that space is flat is
supported by theorists' prejudices and, more importantly, by observations of
fluctuations in the
cosmic
microwave background by
COBE and
other experiments, some of which involve
Jodrell
Bank. (See also the web sites for
MAP and
Planck
Surveyor.) Very recently the
BOOMERANG
and
MAXIMA
experiments have produced beautiful data on
fluctuations in the microwave background on angular scales of the order of a
degree. These provide strong evidence that space really is flat.
exactly
zero. This would also give a flat space (in which a straight line is the
shortest distance between two points). The idea that space is flat is
supported by theorists' prejudices and, more importantly, by observations of
fluctuations in the
cosmic
microwave background by
COBE and
other experiments, some of which involve
Jodrell
Bank. (See also the web sites for
MAP and
Planck
Surveyor.) Very recently the
BOOMERANG
and
MAXIMA
experiments have produced beautiful data on
fluctuations in the microwave background on angular scales of the order of a
degree. These provide strong evidence that space really is flat.
However there are two problems with this picture.
The solution is to reintroduce the cosmological constant. This was first proposed by Einstein as way to cancel the gravitational forces in the universe which, as we have seen, require an expanding universe. He then rejected the idea as his ``biggest blunder'' when Hubble showed that the universe is indeed expanding.
The cosmological constant can be though of as a mass density of the
vacuum (``empty'' space)
If a mass density of empty space isn't weird enough, consider what happens as
space expands. This density is a constant and so as the volume of some
region of space expands so does the total mass contained in it. From special
relativity we know that this extra mass is equivalent to extra energy. If we
are to hold onto the idea of conservation of energy, this energy cannot just be
created. It come from work done on the region of space as it expands.
The vacuum must therefore exert a negative pressure
Although we really need general relativity to calculate the energy of our test
galaxy in the presence of the combined forces of gravity and vacuum pressure,
the final result is deceptively simple:
The net effect of the cosmological constant is to slow the deceleration of the universe. At the present day its effect is almost exactly cancelled by the gravitational attraction between the matter in the universe. However, as the universe continues to expand, matter will get less and less dense and the repulsion will dominate, leading to an ever accelerating expansion. (For more on the cosmological constant, see: Ned Wright's cosmology tutorial, Sean Carroll's encyclopedia article, Eli Michael's web document and John Norbury's course on general relativity.)
Finally, a cosmological constant ![]() may provide the extra mass density
needed to make space flat as well as the repulsive pressure to overcome
gravity, but it also brings its own problems. Why is it there? Why is it so
very small (up to 120 orders of magnitude smaller than estimates of its
natural size in field theories)?
may provide the extra mass density
needed to make space flat as well as the repulsive pressure to overcome
gravity, but it also brings its own problems. Why is it there? Why is it so
very small (up to 120 orders of magnitude smaller than estimates of its
natural size in field theories)?
Textbook references
Home: PC 1672 home page |
Up: 3 Gravity |
Weekly plan |
Help: Guide to using this document |
Next: 4 Rigid-body motion |
Previous: 3.12 Tides |
Mike Birse
17th May 2000