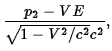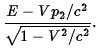Hint 1

(a)

$$p'_1 = p_1,$$

$$p'_2 = {p_2 - VE\over \sqrt{1-V^2/c^2}c^2 },$$

$$p'_3 = p_3,$$

$$E' = {E - Vp_2/c^2 \over \sqrt{1-V^2/c^2} } .$$

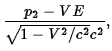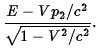(b) ${\bf F}_{\rm cent}=-m\hbox{\boldmath$\omega$ }\times(\hbox{\boldmath$\omega$ } \times{\bf x})$

(c) Zero

(d) See 3.6 Central-force motion

(e) Your diagram should show: the normal to the plate, the line bisecting the plate through the fixed point (axis of symmetry), and the edge on which the fixed point lies (perpendicular to the other two principal axes).