Question 1

(a) The space-time coordinates of a particle in inertial frames $S$ and $S'$ are related by the equations

$$x'_1 = x_1,$$

$$x'_2 = {x_2 - Vt\over \sqrt{1-V^2/c^2} },$$

$$x'_3 = x_3,$$

$$t' = {t - Vx_2/c^2 \over \sqrt{1-V^2/c^2} } .$$

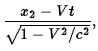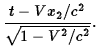If the particle has momentum ${\bf p}= (p_1,p_2,p_3)$ and energy $E$in frame $S$, what are its momentum and energy in frame $S'$?

[5 marks]

(b) Write down the expression for the centrifugal force on a particle of mass $m$ with position ${\bf x}$ and velocity ${\bf v}$ in a frame that is rotating with angular velocity $\hbox{\boldmath$\omega$ }$.

[5 marks]

(c) A car of mass 1500 kg is travelling due N through Ecuador at 100 km/hr. What is the Coriolis force acting on it as it crosses the equator?

[5 marks]

(d) Explain why the radius vector of a planet orbiting the sun sweeps out area at a constant rate.

[5 marks]

(e) Draw a diagram illustrating the set of principal axes of rotation for a uniform square plate rotating about the midpoint of one of its edges.

[5 marks]

[Hints can be found here, but do not follow this link until you have attempted the question on your own.]