Next: 5.3 Bosons and Fermions
Previous: 5.1 The Gibbs Distribution
5.2 Two examples of the Gibbs Distribution
Take-home message: There is an important distinction between systems in which energy levels
can only have one particle in them, and those where they can have many.
Example 1: Sites which bind a single molecule
We first consider sites on a surface which can bind a single molecule only; the energy of the empty site is
0 and that of the occupied site is 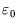 (which can have either sign, but is negative for binding).
This example is common in biology, where receptor molecules can be occupied or unoccupied.
(which can have either sign, but is negative for binding).
This example is common in biology, where receptor molecules can be occupied or unoccupied.
The surface is in contact with a gas or a solution with chemical potential 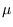 (the energy drop of the solution
when it loses a molecule). What is the grand partition function, and the average occupancy of a site?
(the energy drop of the solution
when it loses a molecule). What is the grand partition function, and the average occupancy of a site?
There are only two microstates here: unoccupied, with 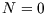 and
and 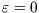 , and occupied, with
, and occupied, with  and
and
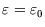 , so there are only two terms in the grand partition function:
, so there are only two terms in the grand partition function:
Then
Below we plot the average occupancy as a function of 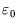 , the energy of the level in question.
, the energy of the level in question.
We see that
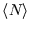 is always less than 1, as it must be. If a level lies above the chemical potential,
is always less than 1, as it must be. If a level lies above the chemical potential,
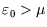 then it is less likely to be occupied, since it is energetically more favourable for the
molecule to remain in solution. Conversely if
then it is less likely to be occupied, since it is energetically more favourable for the
molecule to remain in solution. Conversely if
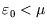 then it is more likely to be occupied, since
that is the energetically favourable configuration. As always, it is the temperature which determines the likelihood
of the less favourable configuration obtaining. At zero temperature, the distribution becomes a step function, with
then it is more likely to be occupied, since
that is the energetically favourable configuration. As always, it is the temperature which determines the likelihood
of the less favourable configuration obtaining. At zero temperature, the distribution becomes a step function, with
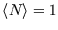 if
if
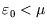 and
and
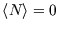 if
if
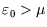 .
.
Example 2: sites which bind many molecules
This is less realistic, but we imagine a site which can have any number of molecules occupying it, with energy
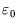 per molecule. There are then infinitely many terms in the grand partition function which
form a geometric series:
per molecule. There are then infinitely many terms in the grand partition function which
form a geometric series:
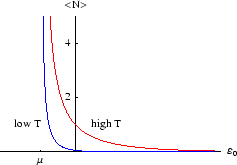
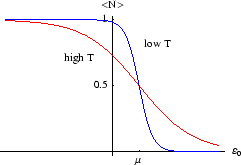
Below we plot the average occupancy as a function of 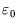 , the energy of the level in question.
, the energy of the level in question.
Unlike the first example, there is no limit to
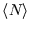 . Thus it doesn't make sense to consider states with
. Thus it doesn't make sense to consider states with
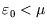 , as their occupancy will be infinite. (The formula above for
, as their occupancy will be infinite. (The formula above for
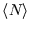 is no longer valid
in that case.) For
is no longer valid
in that case.) For 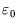 close to
close to 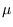 the occupancy will be high, and it falls off as
the occupancy will be high, and it falls off as 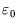 increases. The rapidity of the drop depends on temperature; for
increases. The rapidity of the drop depends on temperature; for 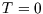 only a level with
only a level with
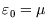 would
have non-zero occupancy.
would
have non-zero occupancy.





Next: 5.3 Bosons and Fermions
Previous: 5.1 The Gibbs Distribution
Judith McGovern
2004-03-17
![]() (which can have either sign, but is negative for binding).
This example is common in biology, where receptor molecules can be occupied or unoccupied.
(which can have either sign, but is negative for binding).
This example is common in biology, where receptor molecules can be occupied or unoccupied.
![]() (the energy drop of the solution
when it loses a molecule). What is the grand partition function, and the average occupancy of a site?
(the energy drop of the solution
when it loses a molecule). What is the grand partition function, and the average occupancy of a site?
![]() and
and ![]() , and occupied, with
, and occupied, with ![]() and
and
![]() , so there are only two terms in the grand partition function:
, so there are only two terms in the grand partition function:
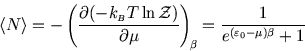
![]() , the energy of the level in question.
, the energy of the level in question.
![]() per molecule. There are then infinitely many terms in the grand partition function which
form a geometric series:
per molecule. There are then infinitely many terms in the grand partition function which
form a geometric series:
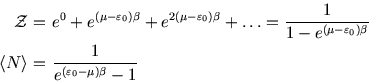
![]() , the energy of the level in question.
, the energy of the level in question.