The grand potential is
So
![]() . Note that two of the variables
. Note that two of the variables ![]() and
and ![]() are intensive,
so
are intensive,
so ![]() , being extensive, must be simply proportional to
, being extensive, must be simply proportional to ![]() , the only extensive one:
, the only extensive one:
![]() .
But
.
But
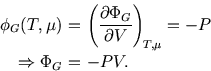
This also follows from the fact that ![]() is just the Gibbs free energy per particle (see here),
so
is just the Gibbs free energy per particle (see here),
so
![]() and hence
and hence
![]() .
.
The fact that ![]() is so
simple doesn't lessen its formal utility in statistical mechanics.
is so
simple doesn't lessen its formal utility in statistical mechanics.