Entropy in a non-isolated system

We can't use an ensemble average directly for the entropy, because it doesn't make sense to talk about the entropy of a microstate. But we can talk about the entropy of the ensemble since the many copies can be in many different microstates. So we define the entropy of the system as the entropy of the ensemble divided by the number of copies, $\nu$, in the ensemble: $\left\langle S \right\rangle =S_\nu/\nu$.

The ensemble has $\nu_i$ copies in the $i$th microstate, so the number of ways of arranging these is

$$\Omega_\nu={\nu!\over \nu_1! \nu_2! \nu_3!\ldots}$$

(compare the ways of arranging counters on the in the chequerboard).

So, using Stirling's approximation,

$$\begin{eqnarray*} \ln\Omega_\nu \!\!\!&=&\!\!\!\nu\ln\nu-\nu-\sum_i(\nu_i\ln\nu_... ..._i\nu_i (\ln\nu_i/\nu) \\ \!\!\!&=&\!\!\!-\nu\sum_i p_i\ln p_i \end{eqnarray*}$$

So the ensemble entropy is $S_\nu=k_{\scriptscriptstyle B}\ln\Omega_\nu$ and the system entropy is

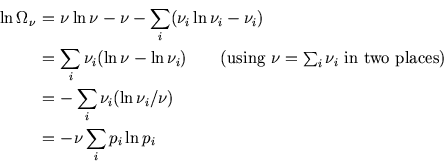
$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle \left\langle S \right\rangle =-k_{\scriptscriptstyle B}\sum_i p_i\ln p_i$ }}$

Note that we have not said anything about what distribution the probabilities $p_i$ follow. For an isolated system, $p_i=1/\Omega$ for each of the $\Omega$ allowed microstates, giving $S=k_{\scriptscriptstyle B}\ln\Omega$ as before.

For a system in contact with a heat bath, $p_i$ is given by the Boltzmann distribution, so

$$\begin{eqnarray*} \left\langle S \right\rangle \!\!\!&=&\!\!\!-k_{\scriptscripts... ...\langle E \right\rangle \over T} +k_{\scriptscriptstyle B}\ln Z \end{eqnarray*}$$

Rearranging we get $k_{\scriptscriptstyle B}T\ln Z=-\left\langle E \right\rangle + T \left\langle S \right\rangle =-\left\langle F \right\rangle$ where $F$ is the Helmholtz free energy, or

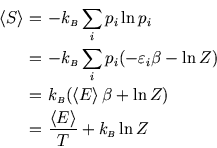
$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle F=-k_{\scriptscriptstyle B}T \ln Z.$ }}$