




Previous: Proof of Clausius's theorem
Increase of entropy
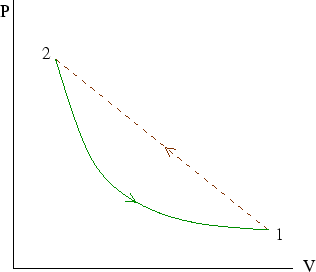
Here we imagine a cycle in which we go from point 1 to point 2 by an irreversible process and back by a
reversible process. (See here for an explanation of the picture.)
The entropy change for a reversible process is given by
What can we say about an irreversible process between the same endpoints? Clearly the entropy change is
the same (that's what we mean by saying entropy is a function of state.) But if we consider a cycle involving
an irreversible process from 1 to 2 and a reversible process to return to 1, we have a cycle for which Clausius's
theorem holds:
Hence in general,
and so for an isolated system, where
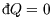 ,
,





Previous: Proof of Clausius's theorem
Judith McGovern
2004-03-17

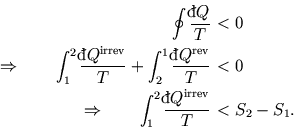
![$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle {\rm d}S\ge 0.
$ }}$](img174.gif)