Proof of Clausius's theorem

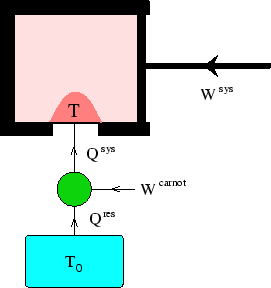
In the diagram, the system is the gas in the piston. We use a Carnot heat engine/pump to add heat $Q^{\rm sys}$ to the system at a local, varying temperature $T$. During the process work $W^{\rm sys}$ is done on the system. (Both $Q^{\rm sys}$ and $W^{\rm sys}$ could be positive or negative.) The cold reservoir of the Carnot engine is at $T_0$.

The Kelvin-Planck statement of the second law says that at the end of a complete cycle of the system, we cannot have extracted net work (or else we would have turned heat from the cold reservoir into work). Looking at the figure to see how the signs of the various works are defined, that means $W^{\rm carnot}+W^{\rm sys}>0$. By conservation of energy, and because the system and engine have returned to their initial states, any net work put in must end up as heat added to the reservoir: $Q^{\rm res}\le 0$ (less than zero because $Q^{\rm res}$ is defined as heat extracted).

Looking now at the Carnot engine, we see that if at some point in the cycle we add heat ${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm sys}$ at temperature $T$, heat ${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm res}$ is extracted from the reservoir, and

$${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm res}={T_... ... T} {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm sys}.$$

Since the total heat extracted is less than zero, we have

$$Q^{\rm res}=\oint {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap... ...e0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm sys}\over T}\le 0$$

which proves the inequality: (dropping the superscript ``sys'')

$$\oint {{}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q\over T }\le 0.$$

Clearly if the system is taken through a reversible cycle, it can be run in reverse and all quantities will simply change signs. But if $Q^{\rm res}$ was less than zero originally, it will be greater for the reversed cycle, implying a net extraction of work and violating the Kelvin-Planck statement. Thus for a reversible system, $Q^{\rm res}$ must be exactly zero, and

$$\oint {{}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm rev}\over T }= 0.$$