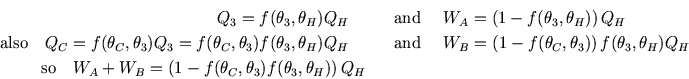Previous: 2.4 Thermodynamic Temperature
Construction of thermodynamic temperature
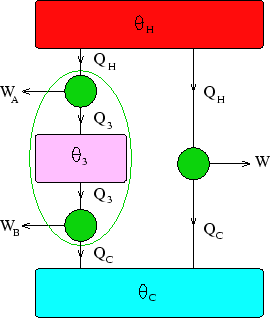
Below we have two engines (one consisting of two more in series)
working between heat reservoirs at 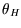 and
and 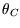 .
Remember
.
Remember 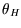 etc refer to temperatures on some unspecified scale. We know that the efficiency
of a Carnot engine working between
etc refer to temperatures on some unspecified scale. We know that the efficiency
of a Carnot engine working between 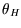 and
and 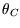 depends only on
depends only on 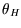 and
and 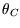 ,
but we don't know how: let us define a function
,
but we don't know how: let us define a function
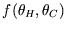 such that
such that
Now considering the two engines in series,
But everything within the green oval in the diagram can be considered as a single, composite, Carnot engine,
so its output must be the same as the simple one for the same heat flow 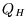 :
: 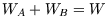 .
Thus we can match the efficiencies of the simple and composite engines to get
.
Thus we can match the efficiencies of the simple and composite engines to get
This has to be true independently of the value of 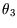 , which can only be true if
, which can only be true if 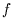 factorises:
factorises:
where 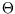 is some function of
is some function of 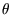
Thus we have the desired result,
References
- Bowley and Sánchez 2.3
- Adkins 4.5-6
- Zemansky 7.5





Previous: 2.4 Thermodynamic Temperature
Judith McGovern
2004-03-17
![]() and
and ![]() .
Remember
.
Remember ![]() etc refer to temperatures on some unspecified scale. We know that the efficiency
of a Carnot engine working between
etc refer to temperatures on some unspecified scale. We know that the efficiency
of a Carnot engine working between ![]() and
and ![]() depends only on
depends only on ![]() and
and ![]() ,
but we don't know how: let us define a function
,
but we don't know how: let us define a function
![]() such that
such that