




Next: 2.5 Entropy
Previous: 2.3 Carnot cycles
2.4 Thermodynamic Temperature
Take-home message: The fact that the efficiency of a Carnot engine depends only on the operating
temperatures provides an alternative way of defining a temperature scale.
If we hadn't already developed a good temperature scale, we could use the fact that the efficiency
of a Carnot engine depends only on the operating temperatures to develop one.
Given a heat bath at a reference temperature (eg a very large triple-point cell) we could use the
efficiency of a Carnot engine working between it and another body to label that other body's temperature.
By considering compound Carnot engines it can be shown that the
dependence of the efficiency on temperature 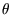 , no matter what scale is used for the latter,
has the form
, no matter what scale is used for the latter,
has the form
where
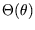 is some function of
is some function of 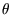 . Thus
. Thus 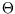 itself is a perfectly good temperature
scale, which vanishes at absolute zero: this is called the thermodynamic temperature.
(See here for details.)
itself is a perfectly good temperature
scale, which vanishes at absolute zero: this is called the thermodynamic temperature.
(See here for details.)
The reason you haven't heard of it is that, if we compare it with the efficiency expressed in terms of the
ideal gas temperature scale,
we see that 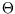 is simply proportional to the ideal gas temperature, and will therefore be identical
if we set
is simply proportional to the ideal gas temperature, and will therefore be identical
if we set
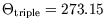 . Since a nearly ideal gas is more achievable than a reversible
heat engine, that's the name that has finally stuck.
. Since a nearly ideal gas is more achievable than a reversible
heat engine, that's the name that has finally stuck.
References
- Bowley and Sánchez 2.3-4
- Adkins 4.6
- Zemansky 7.5
Subsections





Next: 2.5 Entropy
Previous: 2.3 Carnot cycles
Judith McGovern
2004-03-17
![]() , no matter what scale is used for the latter,
has the form
, no matter what scale is used for the latter,
has the form