The N particle partition function for indistinguishable particles.

Before reading this section, you should read over the derivation of $Z_N=(Z_1)^N$ which held for the paramagnet, where all $N$ particles were distinguishable (by their position in the lattice).

Consider first the simplest case, of two particles and two energy levels. If the particles are distinguishable, as in the upper picture below, there are four states, two of which have energy $\varepsilon$, and the two-particle partition function is

$$Z_2= e^0+2e^{-\varepsilon\beta}+e^{-2\varepsilon\beta}=(Z_1)^2$$

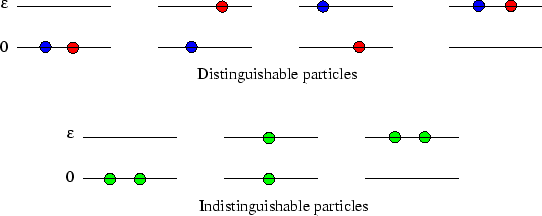
If the particles are indistinguishable, however, there are only three states, as in the lower picture, and the partition function is

$$Z_2= e^0+e^{-\varepsilon\beta}+e^{-2\varepsilon\beta}\ne(Z_1)^2$$

If we use $(Z_1)^2$, we over-count the state in which the particles are in different energy levels. In general there is no simple expression for the $N$-particle partition function for indistinguishable particles.

However we note that $(Z_1)^N$ over-counts the states in which all $N$ particles are in different energy levels by exactly $N!$. So if we are in a position where there are many more accessible energy levels (that is, levels with energy less than a few $k_{\scriptscriptstyle B}T$) than there are particles, the probability of any two particles being in the same energy level is small, and almost all states will have all the particles in different levels. Hence a good approximation is

$$Z_N={(Z_1)^N\over N!}.$$

In the ideal gas, we can calculate the number of levels below, say, $2k_{\scriptscriptstyle B}T$, from $\int_0^{k_{\rm max}} D(k) {\rm d}k$ with $\hbar^2 k_{\rm max}^2/2m=2k_{\scriptscriptstyle B}T$, giving $2.1 n_Q V$. So we see that $n_Q$ is a measure of the number of states available, and we can use the approximation $Z_N=(Z_1)^N / N!$ provided $n_Q V\gg N$ (or $n_Q\gg n$). This is the classical limit.

It is worth noting that, assuming a truly ideal gas which never condenses or solidifies, the Sackur-Tetrode equation is not valid for indefinitely low temperatures. It must be wrong, because as $T\to 0$, $n_Q\to0$ and $S\to -\infty$. But we know that $S\to 0$ as $T\to 0$, because all the particles occupy the lowest energy level. But of course that is exactly the regime in which $Z_N=(Z_1)^N / N!$ is no longer valid.

For a gas with the density of air at STP, $n\approx 3\times 10^{25} {\rm m}^{-3}$. We have $n_Q\approx n$ for $T\approx 10^{-2}$ K, so real gases are essentially always classical.

Note too that $n_Q\approx 1/\lambda^3$, where $\lambda$ is the wavelength of a particle with energy $\frac 3 2 k_{\scriptscriptstyle B}T$. This implies that the classical limit holds if the particle separation is large compared with their wavelength--a reasonable-sounding statement! (See the first tutorial sheet of last semester, PC210 qu. 1(b-d) ).

An example of a non-classical gas is the conduction electrons in a metal; they are free to move within the metal and can be treated as a dense gas ( $n\approx 10^{29} {\rm m}^{-3}$), but at room temperature $n_Q\approx10^{27} {\rm m}^{-3}$. So the quantum nature of the electron (specifically the fact that it is a fermion) becomes all important.