4.3 Entropy, Helmholtz Free Energy and the Partition Function

Take-home message: Once we have the Helmholtz free energy $F$ we can calculate everything else we want.

Here is the crucial equation which links the Helmholtz free energy and the partition function:

$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle F=-k_{\scriptscriptstyle B}T \ln Z$ }}$

The details of the derivation can be found here.

Since $F=E-TS$, from the fundamental thermodynamic relation we obtain ${\rm d}F=-S {\rm d}T-P {\rm d}V+\mu {\rm d}N$. Thus

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle S=-\left... ...splaystyle\mu=\left({\partial F\over\partial N}\right)_{\!\scriptstyle T,V}$}}$

(We first met these in the derivation of Maxwell's relations.) For a magnetic system, we have $m=-\left({\partial F/\partial B}\right)_{\scriptscriptstyle T,N}$ instead of the equation for P.

Remember, $Z$ and hence $F$ depend on $V$ (or $B$) through the energies of the microstates. For instance the energy levels of a particle in a box of side $L$ are proportional to $\hbar^2/(m L^2)\propto V^{-2/3}$.

These relations are reminiscent of those we met in the case of an isolated system, but there the entropy was the key; here it is the Helmholtz free energy. We can make the following comparison:

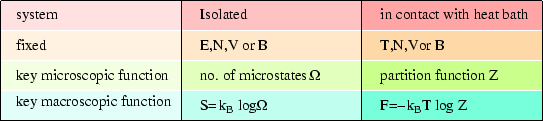
It should not surprise us to find that the Helmholtz free energy is the key to a system at fixed temperature (in contrast to the entropy for an isolated system) as that is what we found classically (see here.)

References

• Mandl 2.5
• (Bowley and Sánchez 5.3-6)
• Kittel and Kroemer 3