2.12 Maxwell's Relations

Take-home message: Remember these relations!

As we have seen, the fundamental thermodynamic relation ${\rm d}E=T{\rm d}S-P{\rm d}V$ implies that the natural variable in which to express $E$ are $S$ and $V$: $E=E(S,V)$.

That means that on purely mathematical grounds, we can write

$${\rm d}E=\left({\partial E\over\partial S}\right)_V{\rm d}S+\left({\partial E\over\partial V}\right)_S{\rm d}V$$

But comparison with the fundamental thermodynamic relation, which contains the physics, we can make the following identifications:

$$T=\left({\partial E\over\partial S}\right)_V\qquad\hbox{and}\qquad P=-\left({\partial E\over\partial V}\right)_S$$

These (especially the second) are interesting in their own right. But we can go further, by differentiating both sides of the first equation by $V$ and of the second by $S$:

$$\left({\partial T \over\partial V}\right)_S =\left({\partia... ...\partial S}\left({\partial E\over\partial V}\right)_S\right)_V$$

Using the fact that the order of differentiation in the second derivation doesn't matter, we see that the right hand sides are equal, and thus so are the left hand sides, giving

$$\left({\partial T \over\partial V}\right)_S=-\left({\partial P\over\partial S}\right)_V$$

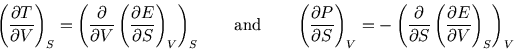
By starting with $F$, $H$ and $G$, we can get three more relations.

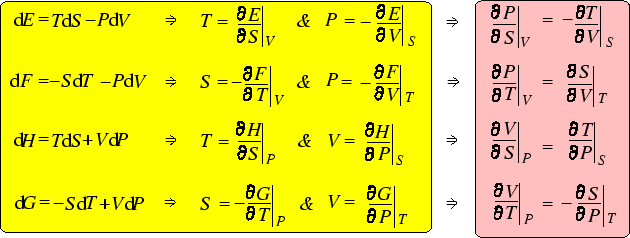
The two equations involving derivatives of $S$ are particularly useful, as they provide a handle on $S$ which isn't easily experimentally accessible.

For non-hydrodynamic systems, we can obtain analogous relations involving, say, $m$ and $B$ instead of $P$ and $V$; for instance by starting with ${\rm d}E=T{\rm d}S+ m{\rm d}B$ we get $(\partial T /\partial B)_S=(\partial m/\partial S)_B$.

To fully exploit these relations, some properties of partial derivatives are useful. See here for a refresher course!

In maths, it's usually quite obvious what the independent variables are: either ${x,y,z}$ or ${r,\theta,\phi}$, for instance, and if you differentiate with respect to one you know that you are keeping the others constant. In thermal physics it isn't obvious at all, so always specify what is being held constant. Expressions like

$${\partial P\over\partial T}\qquad\hbox{and}\qquad{ {\rm d}P\over {\rm d}T}$$

are simply meaningless. (OK, we met the latter in the Clausius-Clapeyron equation, but there it really was the slope of a line: the restriction to points of phase coexistence was understood.)

References

• Mandl 4.1,5
• Bowley and Sánchez 2.6 & E.2
• Adkins 7.3
• Zemansky 10.5