

Next: Hint 2
Up: Examples 4
Previous: Question *9
Hint 1
(a) Each mass is moving with speed
around the axis of rotation. Each has an angular momentum of magnitude
pointing in a direction perpendicular to the rod in the same plane
as 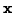 and
and
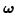 .
Hence the total angular momentum
is
.
Hence the total angular momentum
is
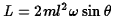 .
It lies at an angle of
.
It lies at an angle of
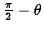 to the axis of rotation.
to the axis of rotation.
(b) The torque needed to maintain this rotation has magnitude
What is its direction?
Mike Birse
2000-03-31