

Next: Hint 5
Up: Examples 3
Previous: Hint 3
Hint 4
Consider a small element of the ring of length
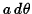 at
an angle
at
an angle 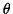 from the line between the centre of the ring and the point
mass. The distance from this element and the point mass is
from the line between the centre of the ring and the point
mass. The distance from this element and the point mass is
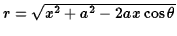 .
Hence, if
.
Hence, if
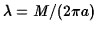 is the linear density of the
ring, the element contributes
is the linear density of the
ring, the element contributes
to the potential energy of the mass. Unlike the example of the spherical shell,
this integral can't be done analytically. However for 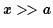 you can make a
Taylor expansion in
you can make a
Taylor expansion in 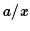 of
of
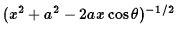 .
If you keep all
terms up to second order in
.
If you keep all
terms up to second order in 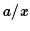 ,
and then integrate, you should get the
result quoted.
,
and then integrate, you should get the
result quoted.
Mike Birse
2000-03-31
![]() at
an angle
at
an angle ![]() from the line between the centre of the ring and the point
mass. The distance from this element and the point mass is
from the line between the centre of the ring and the point
mass. The distance from this element and the point mass is
![]() .
Hence, if
.
Hence, if
![]() is the linear density of the
ring, the element contributes
is the linear density of the
ring, the element contributes