
Next: Hint 2
Up: Examples 3
Previous: Question 11
Hint 1
Use conservation of energy,
to get a first-order differential equation for 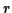 .
Integrating this, you
should find that the time taken is
.
Integrating this, you
should find that the time taken is
The integral can be done by changing variable, with
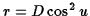 ,
and gives
,
and gives
Mike Birse
2000-03-31