

Next: About this document ...
Up: Examples 2
Previous: Hint 5
Hint 6
Write down the equation of motion from the viewpoint of a frame
rotating with angular velocity 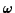 ,
including the centrifugal and
Coriolis terms. Remember to express the inertial-frame velocity appearing the
magnetic part of the force in terms of the velocity in the rotating frame. You
should find that if you choose
,
including the centrifugal and
Coriolis terms. Remember to express the inertial-frame velocity appearing the
magnetic part of the force in terms of the velocity in the rotating frame. You
should find that if you choose
one of the inertial terms exactly cancels the force due to the magnetic field.
The resulting equation of motion should then involve an apparent force that
depends on the particle's position, but not on its velocity:
In a weak magnetic field, you may neglect the final term of order
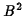 ,
in which case the apparent force is just equal to the original electric
force
,
in which case the apparent force is just equal to the original electric
force 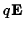 .
The electric field around the proton is given by the usual
inverse-square law. Classically, an electron follows an elliptical orbit in
such a field. (This is just like the corresponding planetary orbits to be
discussed in the Gravitation section of the course.) Now describe how this
motion looks from the standpoint of a nonrotating observer.
.
The electric field around the proton is given by the usual
inverse-square law. Classically, an electron follows an elliptical orbit in
such a field. (This is just like the corresponding planetary orbits to be
discussed in the Gravitation section of the course.) Now describe how this
motion looks from the standpoint of a nonrotating observer.
This effect is known as Larmor precession. Its quantum mechanical
analogue is important in understanding the spectra of atoms in magnetic fields.


Next: About this document ...
Up: Examples 2
Previous: Hint 5
Mike Birse
2000-03-31
![]() ,
in which case the apparent force is just equal to the original electric
force
,
in which case the apparent force is just equal to the original electric
force ![]() .
The electric field around the proton is given by the usual
inverse-square law. Classically, an electron follows an elliptical orbit in
such a field. (This is just like the corresponding planetary orbits to be
discussed in the Gravitation section of the course.) Now describe how this
motion looks from the standpoint of a nonrotating observer.
.
The electric field around the proton is given by the usual
inverse-square law. Classically, an electron follows an elliptical orbit in
such a field. (This is just like the corresponding planetary orbits to be
discussed in the Gravitation section of the course.) Now describe how this
motion looks from the standpoint of a nonrotating observer.