

Next: Hint 5
Up: Examples 2
Previous: Hint 3
Hint 4
The Coriolis force on a falling particle is
as discussed in the lectures. Neglecting effects of order 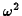 ,
this can
be integrated twice with respect to
,
this can
be integrated twice with respect to 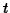 to get the deflection when the
particle has fallen a distance
to get the deflection when the
particle has fallen a distance 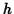 :
:
in the e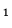 direction (i.e. eastwards). This is in the same direction
as the Earth's motion. Why?
direction (i.e. eastwards). This is in the same direction
as the Earth's motion. Why?
For the numbers given, the deflection is about 1.5 cm.
Mike Birse
2000-03-31