Question 1

[Revision of the relativistic forms for the energy of a particle in terms of its momentum or velocity.]

(a) Write down the relativistic expression for the total energy $E(p)$ of a free particle of mass $m$ moving with momentum $p$.

(b) The relativistic kinetic energy of a particle $T(p)$ is defined as the difference between its total energy $E(p)$ and its rest energy $mc^2$:

$$T(p)=E(p)-mc^2.$$

Show that for small enough $p$, the kinetic energy is given approximately by its nonrelativistic expression

$$T(p)\simeq {p^2\over2m}.$$

What does ``small enough" mean in this context? [Hint: use a Taylor's series to expand $E(p)$ around $p=0$.]

(c) Write down the relativistic expression for the total energy of a free particle of mass $m$ moving with speed $v$. Hence show that the speed of a particle of mass $m$ and energy $E$ is given by

$$v= c\, \sqrt{ 1 - \left({mc^2\over E}\right)^2} .$$

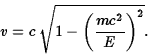
[Hints can be found here, but do not follow this link until you have attempted the question on your own.]