PC1672 Advanced dynamics

2.5 Foucault's pendulum

The small effects of the Coriolis force can also become appreciable if motion persists for a long time. The classic demonstration of this is the pendulum devised by Foucault. This is a very long pendulum, free to swing in any horizontal direction.

In the rotating reference frame of the Earth, the pendulum bob moves under the influence of the horizontal component of the tension in the string and the Coriolis force. The equations describing its motion are

$\displaystyle \ddot x_1-2\Omega \dot x_2+\omega_0^2x_1$ $\textstyle =$ $\displaystyle 0$

$\displaystyle \ddot x_2+2\Omega \dot x_1+\omega_0^2x_2$ $\textstyle =$ $\displaystyle 0$

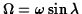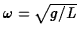The second term in each equation is the Coriolis effect, proportional to the vertical component of the Earth's angular velocity $\Omega=\omega\sin\lambda$ . The last term is the usual restoring force on the bob, with $\omega=\sqrt{g/L}$ being the natural frequency of the pendulum.

The equations are two coupled linear ODE's. To solve them, we take a trial solution of the form

$\begin{displaymath}x_1(t)=X_1e^{{\rm i}\alpha t}\qquad\qquad x_2(t)=X_2e^{{\rm i}\alpha t}\end{displaymath}$

Substituting this into the equations of motion leads to two linear equations which can be written in matrix form as

$\begin{displaymath}\left(\begin{array}{cc} \omega_0^2-\alpha^2&-{\rm i}2\Omega\a... ...ray}\right)\left(\begin{array}{c} X_1\\ X_2\end{array}\right)=0\end{displaymath}$

This is a generalised eigenvalue problem: nontrivial solutions exist only if the determinant of the matrix vanishes. This leads to an auxiliary equation which has four solutions for 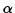$\alpha$ . (Since we started with two second-order ODE's, we expect to have four independent complementary functions.)

A neater approach (used in M) is to combine the two real equations into a single complex one by defining the complex coordinate

$\begin{displaymath}q=x_1+ix_2\end{displaymath}$

The equations of motion can then be written

$\begin{displaymath}\ddot q+{\rm i}2\Omega\dot q+\omega_0^2q=0\end{displaymath}$

In this form the Coriolis term looks like a damping term, except for the fact that its coefficient is imaginary. Using a trial solution of the form

$\begin{displaymath}q(t)=Ae^{{\rm i}\alpha t}\end{displaymath}$

leads to the auxiliary equation

$\begin{displaymath}-\alpha^2-2\Omega\alpha+\omega_0^2=0\end{displaymath}$

This has two roots

$\begin{displaymath}\alpha=-\Omega\pm\sqrt{\omega_0^2+\Omega^2}\end{displaymath}$

Whatever approach we use to solve the equations, we find that they have solutions of the form

$\begin{displaymath}\left(\begin{array}{c}x_1\\ x_2\end{array}\right) =A\left(\be... ...-\sin\Omega t\end{array}\right) \cos\sqrt{\omega_0^2+\Omega^2}t\end{displaymath}$

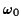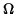These describe oscillations of the pendulum with a frequency that is very close to the natural one $\omega_0$ . The plane of the oscillations precesses at a rate $\Omega$ . In the northern hemisphere, this precession is clockwise as seen from above, reflecting the rightwards deflection of the motion by the Coriolis force. The rate of precession is equal to the vertical component of the Earth's angular velocity. (From an inertial observer's point of view, the pendulum is just trying to keep swinging in the same plane, while the Earth turns underneath it.)

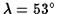Here in Manchester, at latitude $\lambda=53^\circ$ , the rate of precession is

$\begin{displaymath}\Omega=\omega\sin\lambda=12^\circ\hbox{\rm hour}^{-1}\end{displaymath}$

Textbook references

K&K 8.5, example 8.11
F&C 5.5
B&O 7.4
M 11.4, example 11.4(c)
M&T 10.4

Mike Birse
17th May 2000

$\displaystyle \ddot x_1-2\Omega \dot x_2+\omega_0^2x_1$	$\textstyle =$	$\displaystyle 0$
$\displaystyle \ddot x_2+2\Omega \dot x_1+\omega_0^2x_2$	$\textstyle =$	$\displaystyle 0$