PC1672 Advanced dynamics

3.4 Gravitational potentials

The gravitational potential at a point ${\bf x}$ is defined as the potential energy of a unit mass at that point ( $\Phi=U/m$ ). It is related to the gravitational field by

$\begin{displaymath}{\bf g}({\bf x})=-\hbox{\boldmath $\nabla$}\Phi\end{displaymath}$

The potential at a distance

from a point mass

$\begin{displaymath}\Phi=-{GM\over r}\end{displaymath}$

We can calculate the potential due to a general extended body by chopping the body up into small elements which we can treat like point masses. The total potential is then found by summing up (integrating) the potentials of the elements. For a body of volume and density $\rho({\bf x})$ we have

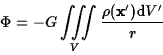
$\begin{displaymath}\Phi=-G\int\!\!\!\int\limits_V\!\!\!\int{\rho({\bf x}'){\rm d}V'\over r}\end{displaymath}$

where

is the distance from the point of interest ${\bf x}$ to an element ${\rm d}V'$ at ${\bf x}'$ .

In the case of a thin spherical shell of matter with mass and radius , we find that the potential at distance from the centre is

$\begin{displaymath}\Phi=-{GM\over x}\end{displaymath}$

if we are outside the shell (

). The gravitational field outside the shell is thus identical to that of a point mass

at the centre. Inside the shell (

) we find that the potential is constant,

$\begin{displaymath}\Phi=-{GM\over a}\end{displaymath}$

and so the field vanishes. These results can be derived either by direct integration or, more elegantly, by using the gravitational version of Gauss's law.

A general spherical distribution of matter can be broken up into to concentric spherical shells. Using the results above we see that only the matter inside a radius contributes to the field at , and that its contribution looks just like that of a point mass at the centre. In terms of the total mass inside radius , the field is

$\begin{displaymath}{\bf g}=-{GM(r)\over r^2}{\bf e}_r\end{displaymath}$

Gauss's law: The gravitational field satisfies Gauss's law in the form

$\begin{displaymath}\int\!\!\!\int{\bf g}\cdot{\rm d}{\bf S}=-4\pi GM_{\rm encl}\end{displaymath}$

or in the equivalent differential form

$\begin{displaymath}\hbox{\boldmath $\nabla$}\cdot{\bf g}=-4\pi G\rho\end{displaymath}$

This can also be expressed as Poisson's equation for the potential

$\begin{displaymath}\nabla^2\Phi=4\pi G\rho\end{displaymath}$

The

potential due to point mass (or a point charge in electrostatics) is an example of a Green's function (in this case for Poisson's equation).

Textbook references

K&K (2.5, note 2.1 discusses the force exerted by a spherical shell of matter)
F&C 6.7 (6.2 for the force exerted by a spherical shell, 6.6 pages 203-204 for galactic rotation and evidence for dark matter)
B&O 8.1 (9.4 for evidence for dark matter)
M 2.8-2.11
M&T 5.2-5.4
B 13.8 (see also 5.4 and 6.10) for the mathematical techniques needed to calculate potentials due to extended bodies

Mike Birse
17th May 2000