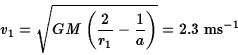

Next: Hint 4
Up: 2000 exam paper
Previous: Hint 2
Hint 3
The pericentre distance is
which corresponds to 190 km above the surface.
The period (which is equal to that for a circular orbit of radius 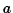 )
is
)
is
since the mass of the asteroid is
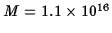 kg.
kg.
The energy (also equal to that for a circular orbit of radius 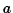 ) is
) is
Hence the energy must decrease by
since the energy of a parabolic orbit is zero.
The maximum speed occurs at pericentre where the energy can be written
Using the total energy above gives
Mike Birse
2001-03-22
![]() )
is
)
is
![]() ) is
) is