




Previous: 1.2 The First Law for Small
Notation for finite and infinitesimal changes
After marking last year's exam, I realised that some students have a problem with the manipulation of finite
and infinitesimal changes. I hope the following helps.
If we are dealing with functions of state, there are three ways they could enter:
- As totals, for instance in the following expressions for a classical ideal gas
- As differentials, for instance in the fundamental thermodynamic relation,
- As finite changes, for instance for a process at constant volume with a heat capacity which
is independent of temperature
There are two basic rules:
- If one term in an equation involves an infinitesimal, all the other terms must also contain one
(and only one!).
- If finite changes are involved, all terms will have reference to the initial and final states.
Introducing things like heat and work which aren't functions of state complicates things slightly;
the first rule still holds (though we write
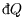 and
and
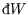 ). However changes in
functions of state can be related to amounts of heat and work, as in
). However changes in
functions of state can be related to amounts of heat and work, as in 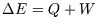 .
.
Another common mistake is to assume that if something involving a differential holds, the
same relation will hold for finite changes. This is not generally true. For instance for an
isothermal expansion of an ideal gas 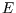 is constant, so
is constant, so
Why not? Well 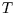 is constant so
is constant so 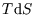 can be integrated to
can be integrated to 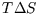 , but
, but 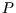 certainly isn't constant so
certainly isn't constant so
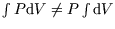 . What we can do here is substitute
. What we can do here is substitute
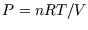 , giving
, giving
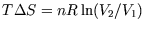 .
.
Similarly,
unless T is constant. However if the heat capacity is constant, as is a reasonably good approximation
for most solids and gases at STP, we can write
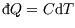 and integrate to get
and integrate to get
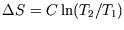 .
.





Previous: 1.2 The First Law for Small
Judith McGovern
2004-03-17
![]() and
and
![]() ). However changes in
functions of state can be related to amounts of heat and work, as in
). However changes in
functions of state can be related to amounts of heat and work, as in ![]() .
.
![]() is constant, so
is constant, so