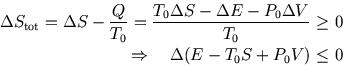Consider a system in thermal contact with its surrounding at ![]() , and at the pressure of the surroundings
, and at the pressure of the surroundings ![]() .
What spontaneous changes will occur? Taking the surroundings and the system together, the entropy will be
maximised.
What does that mean for the system?
.
What spontaneous changes will occur? Taking the surroundings and the system together, the entropy will be
maximised.
What does that mean for the system?
Imagine a spontaneous change during which ![]() is absorbed by the system, and the volume change
is absorbed by the system, and the volume change ![]() , so that
work
, so that
work
![]() is done on the system. Then from the first law,
is done on the system. Then from the first law,
![]() .
The total change in entropy has two parts,
.
The total change in entropy has two parts, ![]() for the system and
for the system and ![]() for the surroundings. So
for the surroundings. So