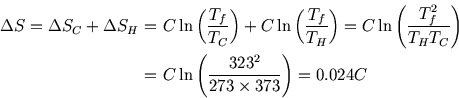Ex. 1

Two identical blocks of iron, one at 100$^{\rm o}$C and the other at 0$^{\rm o}$C, are brought into thermal contact. What happens? What is the total entropy change? (Assume the heat capacity of each block, $c$, is constant over this temperature range, and neglect volume changes)

We know what happens: heat flows from the hot to the cold body till they reach the same temperature; conservation of energy requires that this will be at 50$^{\rm o}$C. Why does heat transfer occur? If heat ${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q$ is transferred from a hot body at $T_H$ to a cold one at $T_C$, the entropy decrease of the hot body is ${\rm d}S_H>-{}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q/T_H$, and the entropy increase of the cold body is ${\rm d}S_C>{}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q/T_C$. So the total entropy change is

$${\rm d}S={\rm d}S_H+{\rm d}S_C>\left({1\over T_C}-{1\over T_H}\right){}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q>0$$

So the decrease in entropy of the hot block is more than compensated by the increase in entropy of the cold block. The spontaneous flow of heat is associated with an overall entropy increase, and the two blocks exchange heat till their combined entropy is maximised.

What is the overall entropy change for the total process? Here we have to use a trick. We can't calculate entropy changes for irreversible processes directly; we need to imagine a reversible process between the same endpoints. For the heating or cooling of a block, this would involve bringing it in contact with a series of heat baths at infinitesimally increasing or decreasing temperatures, so that the temperature difference between the heat bath and the block is always negligible and the entropy change is zero.

During this process, the heat transfer and the infinitesimal temperature change are related by ${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm rev}=C {\rm d}T$ and so

$$\Delta S=\int_1^2 {{}\raise0.44ex\hbox{\bf\symbol{'040}}\lla... ...{T_1}^{T_2} {{\rm d}T\over T}=C \ln\left({T_2\over T_1}\right)$$

Thus the total entropy change is

$$\begin{eqnarray*} \Delta S=\Delta S_C+\Delta S_H\!\!\!&=&\!\!\!C \ln\left({T_f\o... ...\!&=&\!\!\!C \ln \left({323^2\over 273\times373}\right)=0.024 C \end{eqnarray*}$$

Note this is positive, and also that entropy has the same units as heat capacity, Joules/Kelvin.