| $f(t)$ |
$F(s)=\int_0^\infty e^{-st}f(t)dt$ |
Restrictions |
|
| $1$ |
$\frac{1}{s}$ |
$s >0$ |
| $e^{at}$ |
$\frac{1}{s-a}$ |
$ s >a$ |
| $t^n$ |
$\frac{n!}{s^{n+1}}$ |
$ s>0$, $n$ a positive integer |
| $t^{-1/2} $ |
$\sqrt{\frac \pi s}$ |
$ s>0$ |
| $\sin(at)$ |
$ \frac{a}{s^2+a^2}$ |
$ s>0$ |
| $\cos(at)$ |
$ \frac{s}{s^2+a^2} $ |
$s >0$ |
| $\sinh(at)$ |
$ \frac{a}{s^2-a^2}$ |
$ s>a$ |
| $\cosh(at)$ |
$ \frac{s}{s^2-a^2} $ |
$s >a$ |
| $t^n f(t)$ |
$ (-1)^n \frac{d^n}{ds^n}\left(F(s)\right)$ |
$ s>0$, $n$ a positive integer |
| $\frac {f(t)} t$ |
$ \int_s^\infty F(y) dy$ |
$ s>0$ |
| $f(at)$ |
$ \frac 1 a\left(F(\frac s a)\right)$ |
$ s>0$ |
| $f'(t)$ |
$sF(s) - f(0)$ |
$ s>0$ |
| $f''(t)$ |
$s^2F(s) -s f(0)- f'(0)$ |
$ s>0$ |
$\theta(t-t_0)$ |
$\frac{e^{-s t_0}}{s}$ |
$t_0,s >0$ |
| $\theta(t-t_0)f(t-t_0)$ |
$ e^{-st_0}F(s)$ |
$t_0,s>0$ |
| $e^{s_0t} f(t)$ |
$F(s-s_0)$ |
$ s>s_0$ |
| $\delta(t-t_0)$ |
$e^{-s t_0}$ |
$t_0,s >0$ |
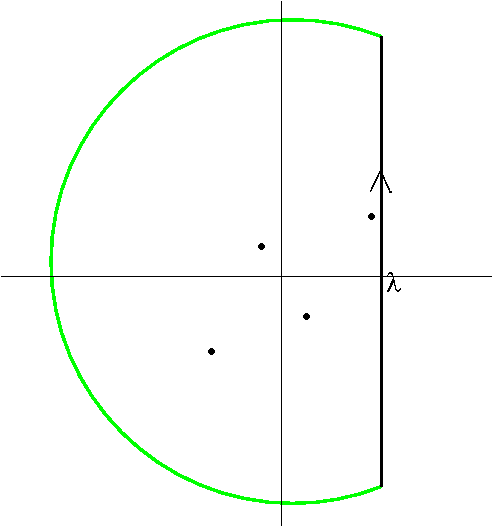 If $F(s)$ has only poles, and no more complicated analytic structure such as branch points, we can close the contour of integration as
shown in the diagram (green arc). Provided $F(s)$ tends to zero as $|s|\to\infty$, if $t>0$ Jordan's Lemma ensures that contribution of
the arc vanishes as the radius is taken to infinity. If $t<0$, we close the contour to the right instead. Hence $f(t)$ is just
given by $\theta(t)$ times the sum of the residues of
$\e^{st} F(s)$. If $F(s)$ has a branch cut the contour will be more complicated.
If $F(s)$ has only poles, and no more complicated analytic structure such as branch points, we can close the contour of integration as
shown in the diagram (green arc). Provided $F(s)$ tends to zero as $|s|\to\infty$, if $t>0$ Jordan's Lemma ensures that contribution of
the arc vanishes as the radius is taken to infinity. If $t<0$, we close the contour to the right instead. Hence $f(t)$ is just
given by $\theta(t)$ times the sum of the residues of
$\e^{st} F(s)$. If $F(s)$ has a branch cut the contour will be more complicated.