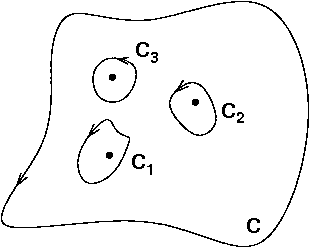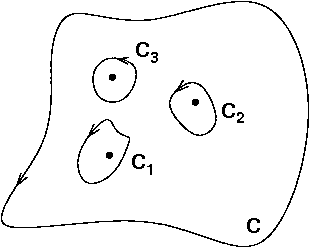PHYS20672 Summary 3
Cauchy's theorem
- Green's theorem in the plane states that for a closed contour $C$ enclosing a surface $S$
$$\oint_C P \d x+Q\d y=\int\int_S\left(\frac{\partial Q}{\partial x}-\frac{\partial p}{\partial y}\right)\d x\d y$$
- Hence Cauchy's theorem: if $f(z)$ is analytic, and so the Cauchy Riemman equations
hold, $$\int f(z) \d z=0$$
- From this it follows that the integral of a function between two points is path independent,
if and only if the function is analytic in the closed region bounded by the two curves.
- If $F(z)=\int_a^z f(\xi)\d\xi$, then $\d F/\d z=f(z)$.
- The indefinite integral $\int^z f(\xi)\d\xi$ doesn't depend on a fixed starting point, and hence is
only defined up to an additive constant.
- If a function is analytic in some region, a closed contour can be deformed at will within that region
without changing the value of the integral along it.
- If a function within a countour is analytic except at a finite number of isolated points
(a meromorphic function), the integral round that contour is the same as the sum of the integrals round
a set of contours each of which circles just one singularity. In the diagram below,
$\oint_C\to\oint_{C_1}+\oint_{C_2}+\oint_{C_3}$.
- $\oint 1/(z-a)\d z=2\pi i$; $\oint 1/(z-a)^n\d z=0$ for integer $n>1$.
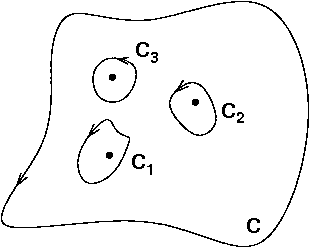
Spiegel 4.9,4.11,4.13-15
Riley 18.11; Boas 14.3; Arfken 6.3