Scattering from a ﬁnite square barrier or well

5.3.2 Scattering from a ﬁnite square barrier or well

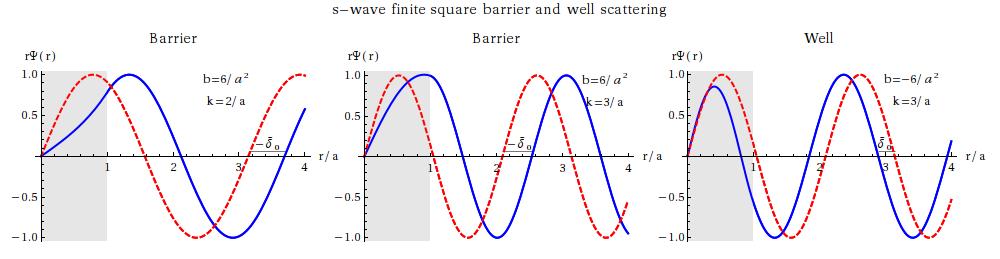
Here we are dealing with $V (r) = 0$ for $r > a$ , and $V (r) = V_{0}$ for $r < a$ , where $V_{0}$ can be greater than zero (a barrier, repulsive) or less (a well, attractive). It will be useful to deﬁne the quantity $b = 2 m V_{0} ∕ ℏ^{2}$ , which has dimesions of inverse length squared. Note that as we are working in 3D the wells and barriers are all spherical.

In this case the wave function will again be $C_{l} j_{l} (k r) + D_{l} n_{l} (k r)$ for $r > a$ , and again $δ_{l} = arctan (- D_{l} ∕ C_{l})$ . However this time the wave function for $r < a$ doesn’t vanish, but has the form $A_{l} j_{l} (k^{'} r)$ where $k^{'} = \sqrt{k^{2} - b}$ and we ﬁnd $D_{l} ∕ C_{l}$ by matching the wave function and its derivative at $r = a$ . Examples of the resulting wavefunctions are shown below, ﬁrst for a barrier with $k < \sqrt{b}$ , then a barrier with $k > \sqrt{b}$ , then a well. As before blue indicates the wavefuntion in the presence of the potential and red (dashed) in its absence. In the ﬁrst two cases the repulsive barrier “pushes the wave outwards” and the phase-shift is negative, in the third the well “draws the wave inwards” and the phase-shift is positive. (Note: what is marked as “ $δ$ ” on the plots is actually $δ ∕ k a$ — a given distance on the graph will represent a larger phase shift if $λ$ is small.)

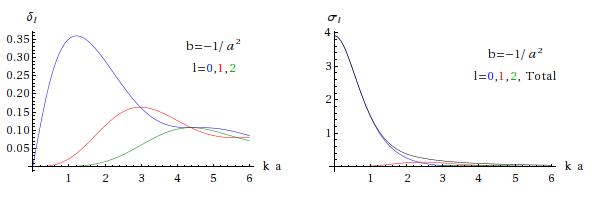
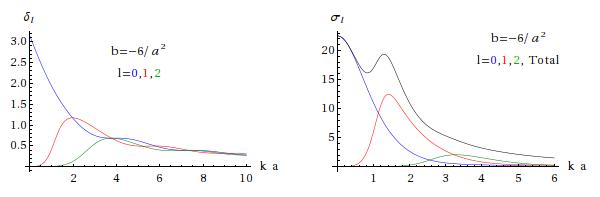
The next two pictures show phase-shifts and cross sections for repulsive potentials (barriers), with the lower one being stronger that the upper one. As expected the phase-shifts start at zero and are negative; as in the hard-sphere case the magnitudes grow initially, but as $k$ increases the barrier gradually becomes less and less signiﬁcant and the phase-shifts and cross sections fall oﬀ to zero.

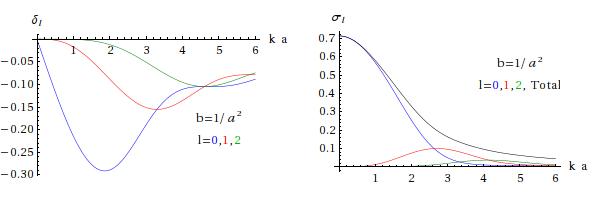
The next two pictures show attractive potentials, and as expected the phase shifts are positive and they and the cross sections fall to zero as $k \to \infty$ .

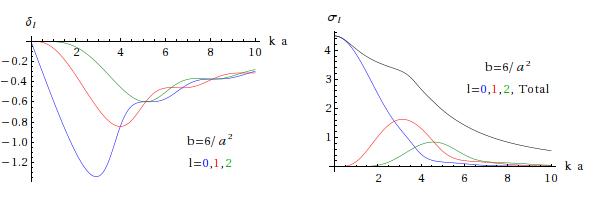
For the weaker well (top) the phase shifts start at zero at $k = 0$ as expected, but for the stronger well the s-wave phase-shift has jumped to $π$ . Why is this? First, we should remember that since we determined $δ$ via an arctangent, it was ambiguous up to a multiple of $π$ . (Another way of seeing that is to recognise that the wave function itself is only deﬁned up to an overall sign.) The correct value can be determined by examining pictures of wavefunctions (if we know the exact solutions as here), or by requiring $δ$ to be a continuous function of $k$ , falling to zero as $k \to \infty$ . Below the wave functions are shown for low $k$ and well depths either side of the critical value; in the second $- ψ$ is shown by the blue dotted line, and it is this which when compared with the red dashed line gives a positive phase shift of more than $π ∕ 2$ (rather than a smaller negative shift of $δ - π$ ).

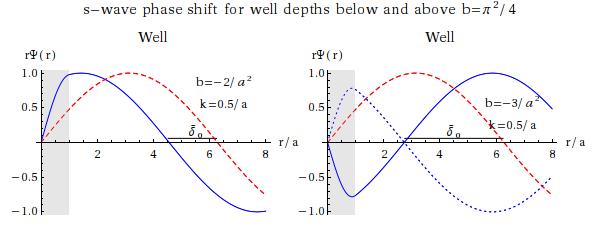
What determines the critical value? A ﬁnite square well in 3D has a zero-energy zero-energy bound-state (i.e. states that would be bound if the well were inﬁnitesimally deeper) if $\sqrt{b} = (2 n + 1) π ∕ 2 a$ , $n = 0, 1, 2 \dots$ . The lowest of these is $b = 2.467 ∕ a^{2}$ , and that is the value at which the phase shift at $k = 0$ jumps from 0 to $π$ . This is an example of Levinson’s theorem, which says that for well-behaved ﬁnite-range potentials the value of the phase-shift $δ_{l}$ at the origin is $n π$ where $n$ is the number of bound states of the potential with angular momentum $l$ . This is an example of how we can obtain information about the potential from scattering.

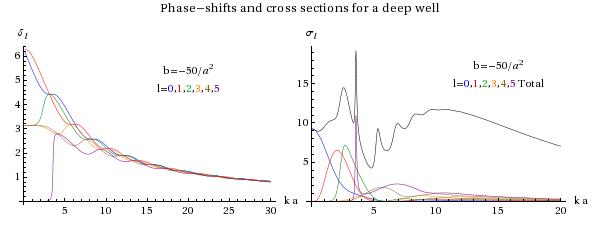
This plot shows a much deeper well. From this we can deduce that for $b = - 50 ∕ a^{2}$ there are two bound states with $l = 0$ , two with $l = 1$ , one each with $l = 2, 3$ and 4, but none with $l = 5$ (or higher). We can also see that for $k$ greater than around $5 ∕ a$ the partial wave description becomes too cumbersome - dozens of partial waves have to be included to reproduce the cross section - far more than could realistically be deduced from experiment.

The plot above also suggests that something interesting is happening around $k = 3.5 ∕ a$ , where there is a very sharp peak in the cross section. It comes from the $l = 5$ partial wave, where the phase-shift rises very rapidly from around 0 to nearly $π$ . Since the cross section is proportional to ${sin}^{2} δ_{l}$ we see that it will rise and fall rapidly over the region in $k$ , peaking at $δ_{l} = π ∕ 2$ . What is happening here is suggested by the next plot, of the $l = 5$ wave function:

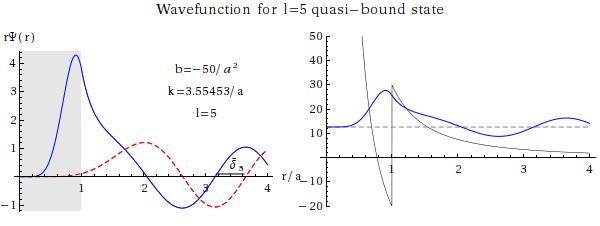
We can see that for $l > 0$ , the combination of the square well and the centrifugal barrier allows for quasi-bound states to form with energies greater than zero — very similar to the situation with radioactive decay, in which $α$ particles were trapped for a time by the Coulomb repulsion (see 2.4.2). When we send in a beam of particles, they will tend to get trapped and the wave function within the well will be large. This is called a resonance. We can’t see the wavefunction, of course, but the clue is in the phase shift, which rises rapidly through $π ∕ 2$ as we scan the energy across the peak. As a function of $k$ , the phase shift and cross section will have the form

δ_{l} = δ_{b} + arctan (\frac{Γ ∕ 2}{E_{r} - E}) σ_{l} = \frac{4 π}{k^{2}} \frac{Γ^{2} ∕ 4}{{(E - E_{r})}^{2} + Γ^{2} ∕ 4}

This is a Lorentzian (ignoring the relatively slowly varying factor of $k^{- 2}$ ) and in the context of scattering it is termed a Breit-Wigner curve. The width $Γ$ gives the lifetime of the quasi-bound state.

The phase shift is very useful for distinguishing random bumps in the cross section from true resonances. For instance when $b$ is just too low for there to be a zero-energy $s$ -wave bound state there will be a signiﬁcant bump in the cross section, but it is not a resonance: there is no centrifugal barrier to trap the particles. (Many text-books fudge this issue, since $l > 0$ is hard to deal with analytically. The correct term for a not-quite-bound state is a virtual state.) In the plot for $b = - 50$ , we can see a number of bumps; the one at $k a \approx 2.5$ might be a $d$ -wave virtual state, but only the really sharp peak at $k a \approx 3.5$ is a resonance. Examples of resonances in particle physics are the $Δ$ , a sort of excited proton, which shows up very strongly in $p$ -wave $π$ N scattering, and the Z-boson which was seen in e $^{+}$ e $^{-}$ scattering at LEP.

Low-energy nucleon-nucleon scattering shows nice examples of both resonances and virtual states:

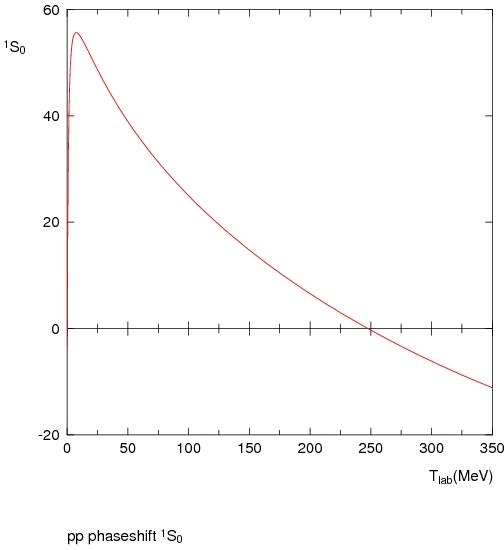
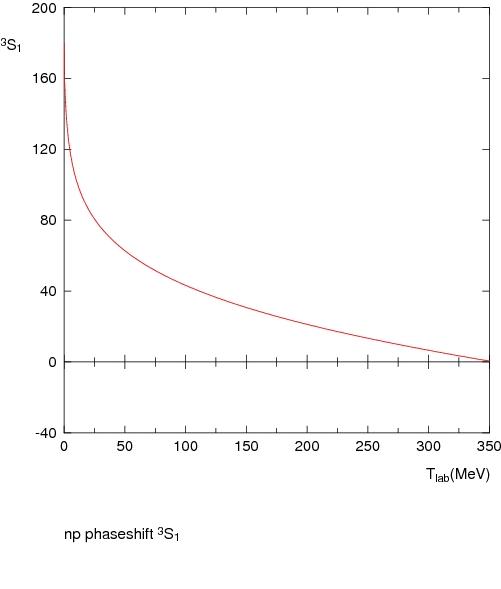
The phase shift is given in degrees. (Note the potential is more complicated than a square well!). In the proton-proton channel there is a virtual state, but no resonance or bound state. If the nuclear force were a little stronger perhaps di-protons could exist. In the neutron-proton channel though the phase shift starts at $π$ ( $18 0^{\circ}$ ) indicating the presence of a bound state — the deuteron. (Plots are from the Nijmegen phase shift analysis of nucleon-nucleon scattering.) The fact that the phase shift starts to go negative at high-enough energy suggests that there is a repulsive hard core to the interaction (as indeed we know from the size of nuclei that there must be).

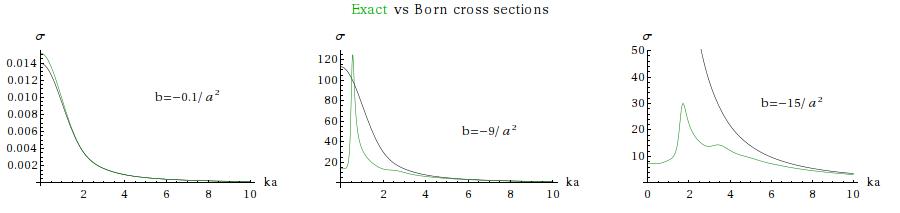
It can be shown (see examples) that the Born approximation is good for high-enough energy scattering ( $k ≫ b a$ ), and the shallower the well the greater its domain of validity till if $b a^{2} ≪ 1$ it will be good everywhere. In the latter case the potential will not have any bound states or resonances. Where the Born approximation breaks down, it is clear that multiple interactions must be important (see 4.7).

[prev] [up] [top]