5.3.1 Hard sphere scattering

For hard sphere scattering, the potential is infinite for $r<a$ and zero for $r>a$. The free form of the wavefuntion therefore holds for all $r>a$, and the wavefunction must vanish at the surface ($r=a$). Since the partial waves are all independent, this means each partial wave must vanish at $r=a$, ie $C_l{j}_l\left(ka\right)+D_l{n}_l\left(ka\right)=0$. Thus

For $l=0$ this is very simple: ${\delta }_l=-ka$. For higher $l$ it has to be solved numerically.

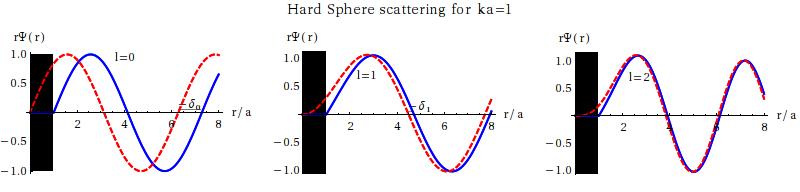
In this figure above we see the corresponding wave functions, blue with the potential and red (dashed) in its absence. The phase shifts ${\delta }_l$ are the displacements between the two.

The graph below shows the phase-shifts and cross sections for this case.

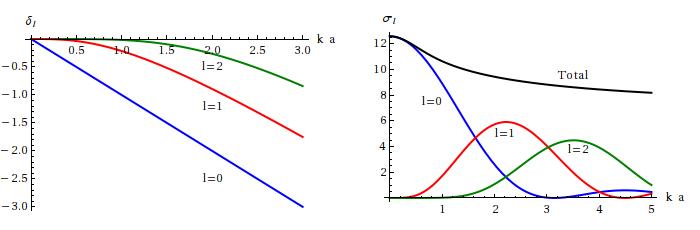
The fact that the phase-shifts are negative indicates a repulsive potential. The fact that the phase-shifts and cross sections don’t tend to zero as $k\to \infty$ is atypical, and comes from the potential being infinite - we can’t use the Born approximation here either.

Since as $z\to 0$, $j_l\left(z\right)∕n_l\left(z\right)\sim z^{2l+1}$, in the low-energy limit $ka\ll 1$ all higher phase shifts are negligible. Then $\sigma \approx {\sigma }_0=4\pi a^2{sinc}^2\left(ka\right)$ which tends to 4 times the classical limit of $\pi a^2$. In the high-energy limit $ka\gg 1$, all phase shifts up to $l\sim ka$ will be significant, and if there are enough of them the average value of ${sin}^2{\delta }_l$ will just be $\frac{1}{2}$. Then we have $\sigma =\frac{2\pi a^2}{{\left(ka\right)}^2}{\sum }_{l=0}^{ka}\left(2l+1\right)\to 2\pi a^2$. We might have expected $\pi a^2$ in this, the classical, limit, but wave optics actually predicts the factor of 2, a phenomenon related to Poisson’s spot.

[next] [up] [top]