WKB approximation for tunnelling

2.4.2 WKB approximation for tunnelling

For the WKB approximation to be applicable to tunnelling through a barrier, we need as always $|λ^{'}| ≪ 1$ . In practice that means that the barrier function is reasonably smooth and that $E ≪ V (x)$ . Now it would of course be possible to do a careful calculation, writing down the WKB wave function in the three regions (left of the barrier, under the barrier and right of the barrier), linearising in the vicinity of the turning points in order to match the wave function and its derivatives at both sides. This however is a tiresomely lengthy task, and we will not attempt it. Instead, recall the result for a high, wide square barrier; the transmission coeﬃcient in the limit $e^{- 2 κ Δ L} ≪ 1$ is given by

T = \frac{16 k_{1} k_{2} κ^{2}}{(κ^{2} + k_{1}^{2}) (κ^{2} + k_{2}^{2})} e^{- 2 κ L}

where $k_{1}$ and $k_{2}$ are the wavenumbers on either side of the barrier (width $L$ , height $V$ ) and $κ = \sqrt{2 m (V - E)}$ . (See the notes for PHYS20101, where however $k_{1} = k_{2}$ .) All the prefactors are not negligible, but they are weakly energy-dependent, whereas the $e^{- 2 κ L}$ term is very strongly energy dependent. If we plot $log T$ against energy, the form will be essentially $const - 2 κ (E) L$ , and so we can still make predictions without worrying about the constant.

For a barrier which is not constant, the WKB approximation will yield a similar expression for the tunnelling probability:

T = [prefactor] \times exp (- 2 \int_{a}^{b} κ (x^{'}) d x^{'})

where $κ (x) \equiv \sqrt{2 m (V (x) - E)} ∕ ℏ$ . The WKB approximation is like treating a non-square barrier like a succession of square barriers of diﬀerent heights. The need for $V (x)$ to be slowly varying is then due to the fact that we are slicing the barrier suﬃciently thickly that $e^{- 2 κ Δ L} ≪ 1$ for each slice.

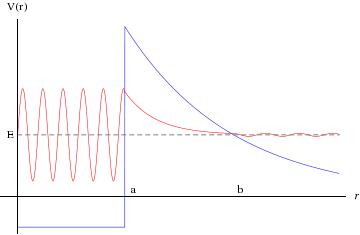
The classic application of the WKB approach to tunnelling is alpha decay. The potential here is a combination of an attractive short-range nuclear force and the repulsive Coulomb interaction between the alpha particle and the daughter nucleus. Unstable states have energies greater than zero, but they are long-lived because they are classically conﬁned by the barrier. (It takes some thought to see that a repulsive force can cause quasi-bound states to exist!) The semi-classical model is of a pre-formed alpha particle bouncing back and forth many times ( $f$ ) per second, with a probability of escape each time given by the tunnelling probability, so the decay rate is given by $1 ∕ τ = f T$ . Since we can’t calculate $f$ with any reliability we would be silly to worry about the prefactor in $T$ , but the primary dependence of the decay rate on the energy of the emitted particle will come from the easily-calculated exponential.

In the ﬁgure above the value of $a$ is roughly the nuclear radius, and $b$ is given by $V_{C} (b) = E$ , with the Coulomb potential $V_{C} (r) = z Z ℏ c α ∕ r$ . ( $Z$ is the atomic number of the daughter nucleus and $z = 2$ that of the alpha.) The integral in the exponent can be done (see Gasiorowicz Supplement 4 B for details; the substitution $r = b {cos}^{2} θ$ is used), giving in the limit $b ≫ a$

2 \int_{a}^{b} κ (x^{'}) d x^{'} = 2 π z Z α \sqrt{\frac{m c^{2}}{2 E}} = 39 \frac{Z}{\sqrt{E (MeV)}} \Rightarrow {log}_{10} \frac{1}{τ} = const - 1.72 \frac{Z}{\sqrt{E (MeV)}}

Data for the lifetimes of long-lived isotopes (those with low-energy alphas) ﬁt such a functional form well, but with $1.61$ rather than $1.72$ . In view of the fairly crude approximations made, this is a pretty good result. Note it is independent of the nuclear radius because we used $b ≫ a$ ; we could have kept the ﬁrst correction, proportional to $\sqrt{b ∕ a}$ , to improve the result.

Gasiorowicz Supplement 4 B
Shankar ch 16.2

[prev] [up] [top]