Variational methods: ground state

2.1 Variational methods: ground state

Summary: Whatever potential we are considering, we can always obtain an upper bound on the ground-state energy.

Suppose we know the Hamiltonian of a bound system but don’t have any idea what the energy of the ground state is, or the wave function. The variational principle states that if we simply guess the wave function, the expectation value of the Hamiltonian in that wave function will be greater than the true ground-state energy:

\frac{⟨ Ψ | \hat{H} | Ψ ⟩}{⟨ Ψ | Ψ ⟩} \geq E_{0}

This initially surprising result is more obvious if we consider expanding the (normalised) $| Ψ ⟩$ in the true energy eigenstates $| n ⟩$ , which gives $⟨ \hat{H} ⟩ = \sum_{n} P_{n} E_{n}$ . Since all the probabilities $P_{n}$ are non-negative, and all the $E_{n}$ greater than or equal to $E_{0}$ , this is obviously not less than $E_{0}$ .

It is also clear that the better the guess (in the sense of maximising the overlap with the true ground state) the lower the energy bound, till successively better guesses converge on the true result.

As a very simple example, consider the inﬁnite square well with $V = 0, 0 < x < a$ and $V = \infty$ otherwise. As a trial function, we use $Ψ (x) = x (a - x), 0 < x < a$ and $Ψ (x) = 0$ otherwise. Then

\frac{⟨ Ψ | \hat{H} | Ψ ⟩}{⟨ Ψ | Ψ ⟩} = \frac{10 ℏ^{2}}{2 m a^{2}} = 1.013 \frac{π^{2} ℏ^{2}}{2 m a^{2}}

This is spectacularly good! Obviously it helped that our trial wave function looked a lot like what we’d expect of the true solution - symmetric about the midpoint, obeying the boundary conditions, no nodes....

In general, we will do better if we have an adjustable parameter, because then we can ﬁnd the value which minimises our upper bound. So we could try $Ψ (x) = x (a - x) + b x^{2} {(a - x)}^{2}$ (with our previous guess corresponding to $b = 0$ ). Letting Mathematica do the dirty work, we get an energy bound which is a function of $b$ , which takes its minimum value of $1.00001 E_{0}$ at $a^{2} b = 1.133$ . Not much room for further improvement here!

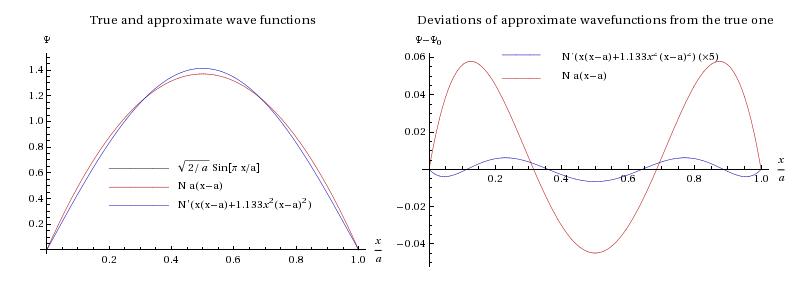
Above we have plotted, on the left, the true and approximate wave functions (except that the true one is hidden under the second approximation, given in blue) and on the right, the deviations of the approximate wave functions from the true one (except that for the second approximation the deviation has been multiplied by 5 to render it visible!) This illustrates a general principle though: the wave function does have deviations from the true one on the part-per-mil scale, while the energy is good to 1 part in $1 0^{5}$ . This is because the error in the energy is proportional to the coeﬃcients squared of the admixture of “wrong” states, whereas the error in the wave function is linear in them.

Another example, for which the analytic solution is not known, is the quartic potential, $V (x) = β x^{4}$ . Here a Gaussian trial wave function $Ψ (x) = e^{- a x^{2} ∕ 2}$ gives an upper bound for the ground energy state of $\frac{3}{8} 6^{1 ∕ 3} = 0.68$ in units of ${(ℏ^{4} β ∕ m^{2})}^{1 ∕ 3}$ . (The value obtained from numerical solution of the equation is $0.668$ ).

Gasiorowicz ch 14.4
Mandl ch 8.1
Shankar ch 16.1

[next] [up] [top]