A.8 Properties of $\delta$-functions

The $\delta$-function is only defined by its behaviour in integrals:

where the limits $a$ and $b$ are positive and as large or small as we want; the integration simply has to span the point on which the $\delta$-function is centred.

The following equivalences may also be proved by changing variables in the corresponding integral (an appropriate integration range is assumed for compactness of notation):

Note that the dimensions of a $\delta$-function are the inverse of those of its argument, as should be obvious from the first equation.

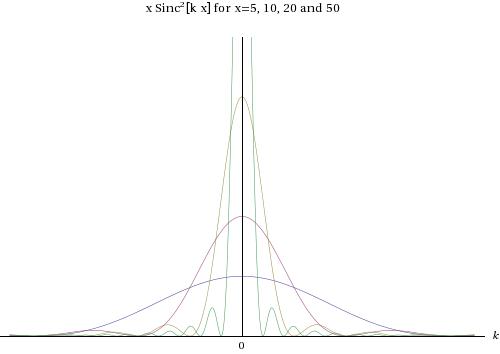
We encounter two functions which tend to $\delta$-functions:

In both cases, as $x\to \infty$ the function tends to zero unless $k=k^{\prime }$, at which point it tends to $x$, so it looks like an infinite spike at $k=k^{\prime }$.

That the normalisation (with respect to integration w.r.t $k$) is correct follows from the following two integrals: ${\int \; <!--nolimits-->}_{-\infty }^{\infty }\text{sinc}\left(t\right)\text{d}t=\pi$ and ${\int \; <!--nolimits-->}_{-\infty }^{\infty }{\text{sinc}}^2\left(t\right)\text{d}t=\pi$. The second of these follows from the first via integration by parts. The integral ${\int \; <!--nolimits-->}_{-\infty }^{\infty }\text{sinc}\left(t\right)\text{d}t=\Im {\int <!--nolimits-->}_{-\infty }^{\infty }{\text{e}}^{it}∕t\text{d}t$ may be done via the contour integral below:

As no poles are included by the contour, the full contour integral is zero. By Jordan’s lemma the integral round the outer circle tends to zero as $R\to 0$ as ${\text{e}}^{iz}$ decays exponentially in the upper half plane. So the integral along the real axis is equal and opposite to the integral over the inner circle, namely $\frac{1}{2}$ of the residue at $x=0$, $i\pi$. So the imaginary part, the integral of $\text{sinc}\left(x\right)$, is $\pi$.

[next] [prev] [up] [top]